An Attempt At Demystifying Bayesian Deep Learning
Eric J. Ma
ericmjl
PyData NYC 2017
Follow along!
On your phone
On your laptop
https://ericmjl.github.io/bayesian-deep-learning-demystifiedThe Hype of Deep Learning:
— Ferenc Huszár (@fhuszar) November 23, 2017
1. Write a post with ML, AI or GAN in the title.
2. post appears at the top of hackernews (despite your best efforts)
3. HN drives tens of thousands of clicks
4. "what's with all the maths? show me pretty pics"
5. <=1% stay for longer than a minute
I am out to solve Point 4.
The Obligatory Neon Bayes Rule Sign
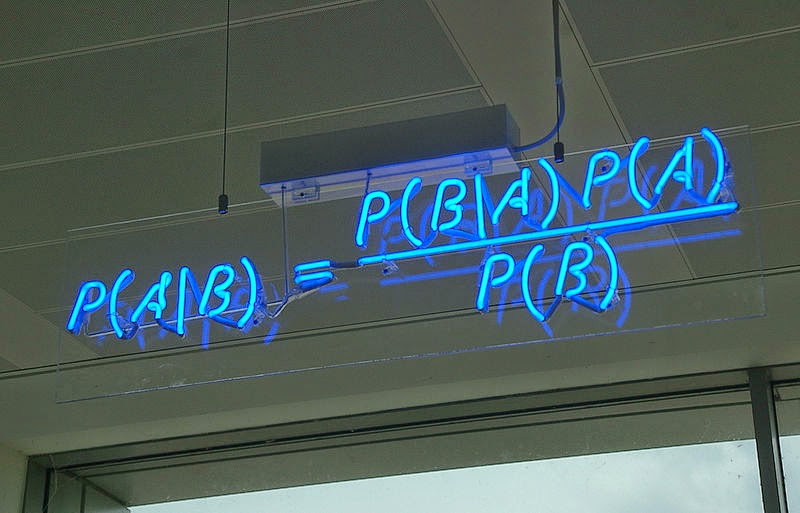
My (Modest) Goals
- Demystify Deep Learning
- Demystify Bayesian Deep Learning
Basically, explain the intuition clearly with minimal jargon.
Take-Home Point 1
Deep Learning is nothing more than compositions of functions on matrices.
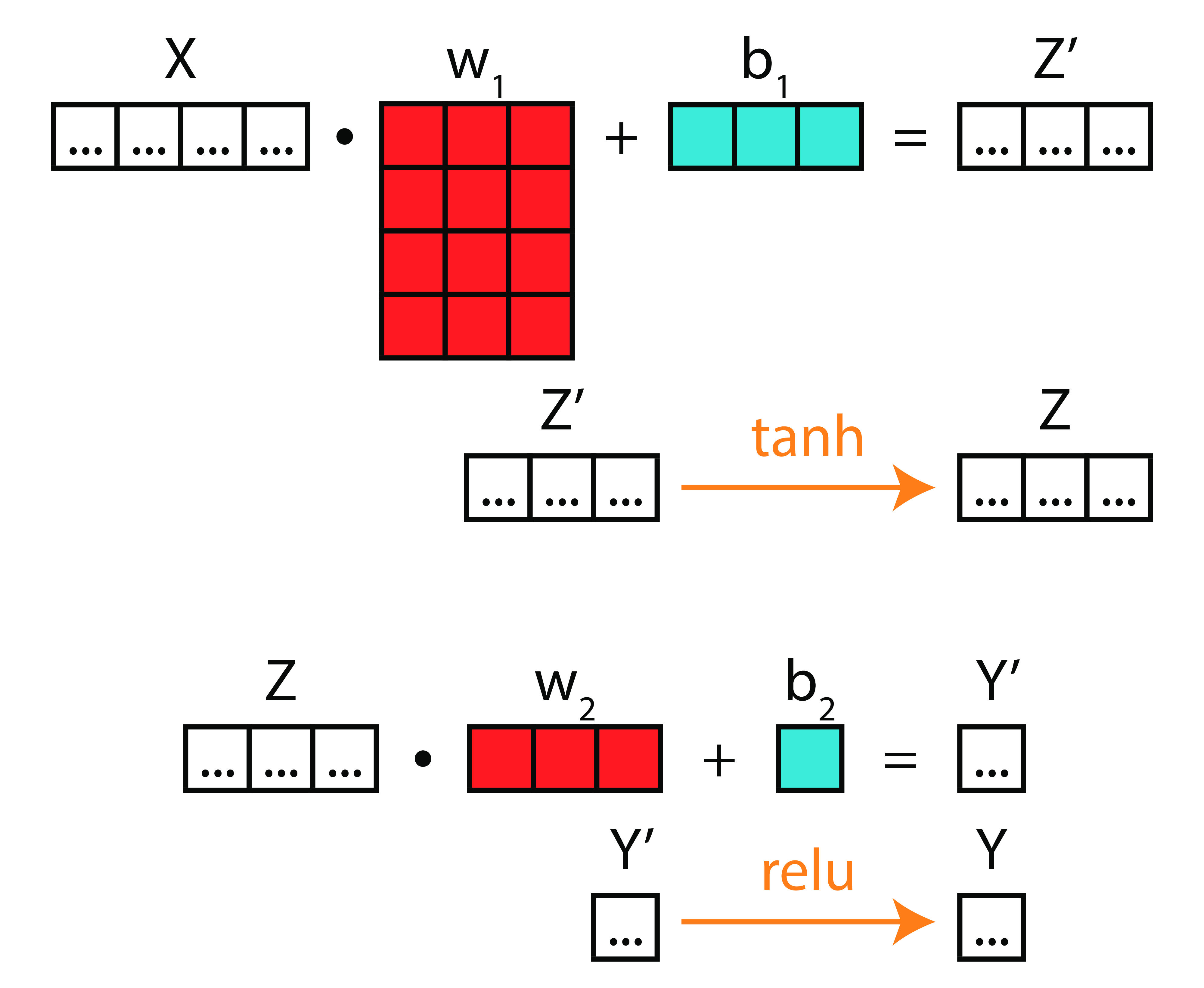
Take-Home Point 2
Bayesian deep learning is grounded on learning a probability distribution for each parameter.
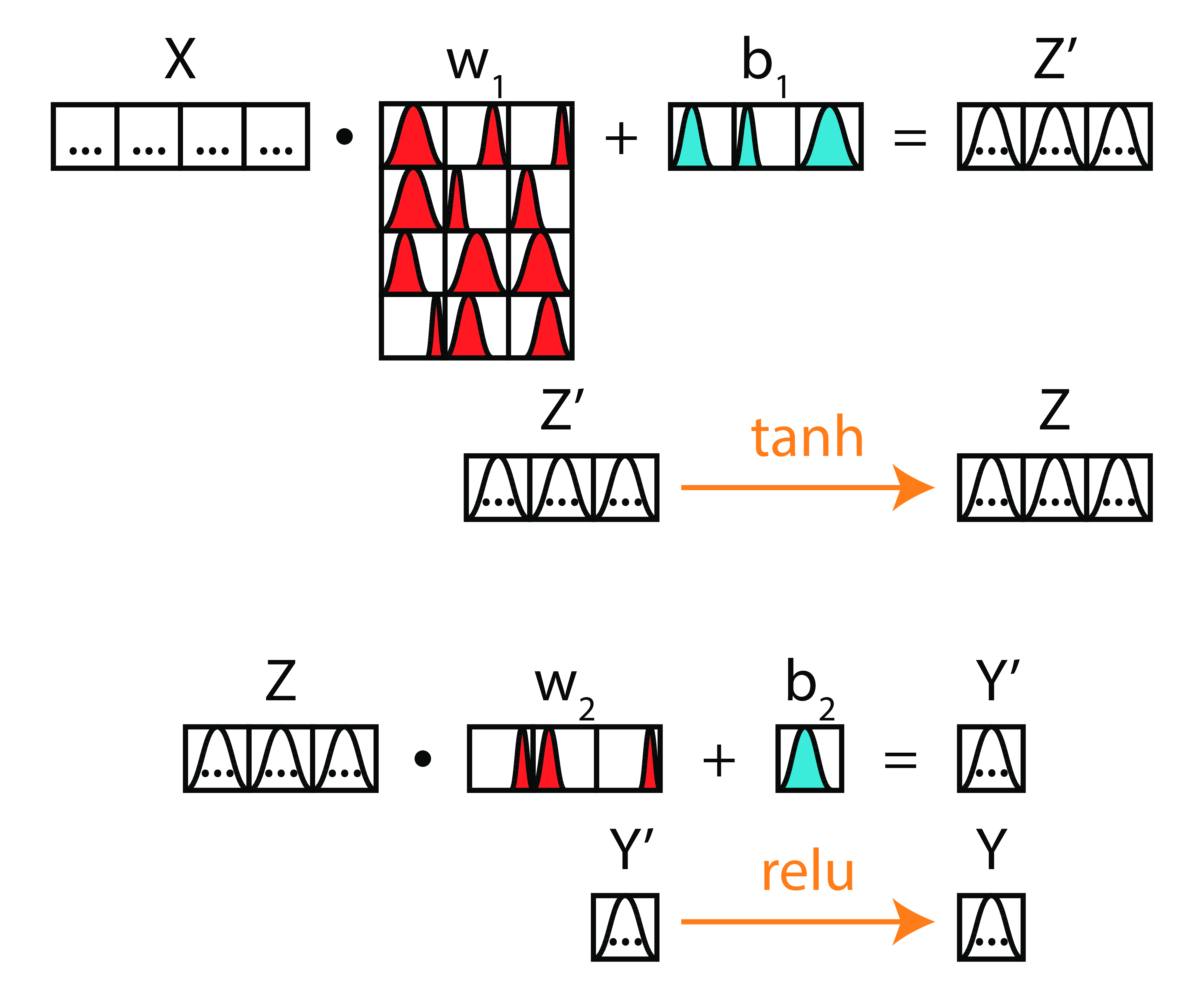
Outline
- Linear Regression 3 Ways
- Logistic Regression 3 Ways
- Deep Nets 3 Ways
- Going Bayesian
- Example Neural Network with PyMC3
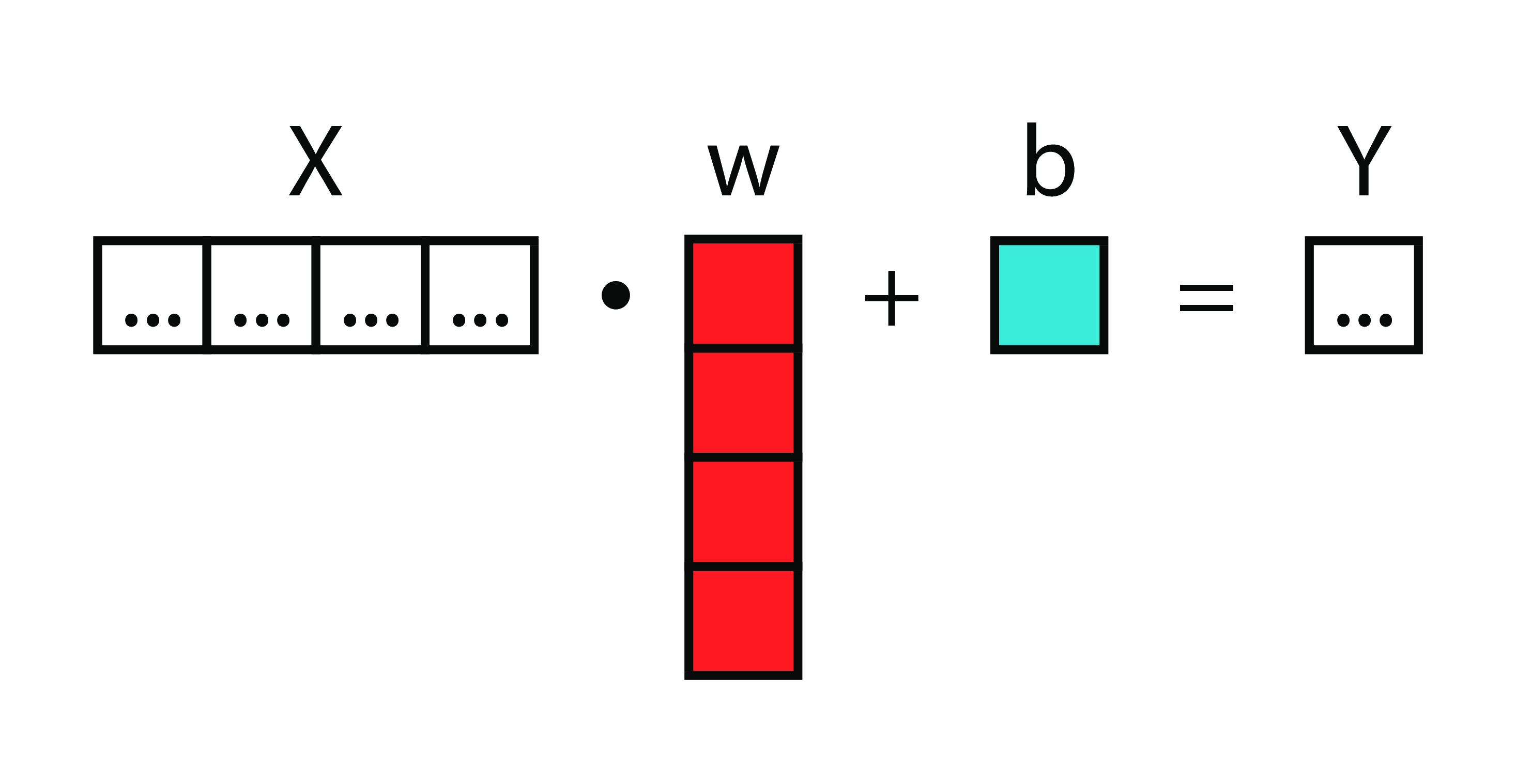
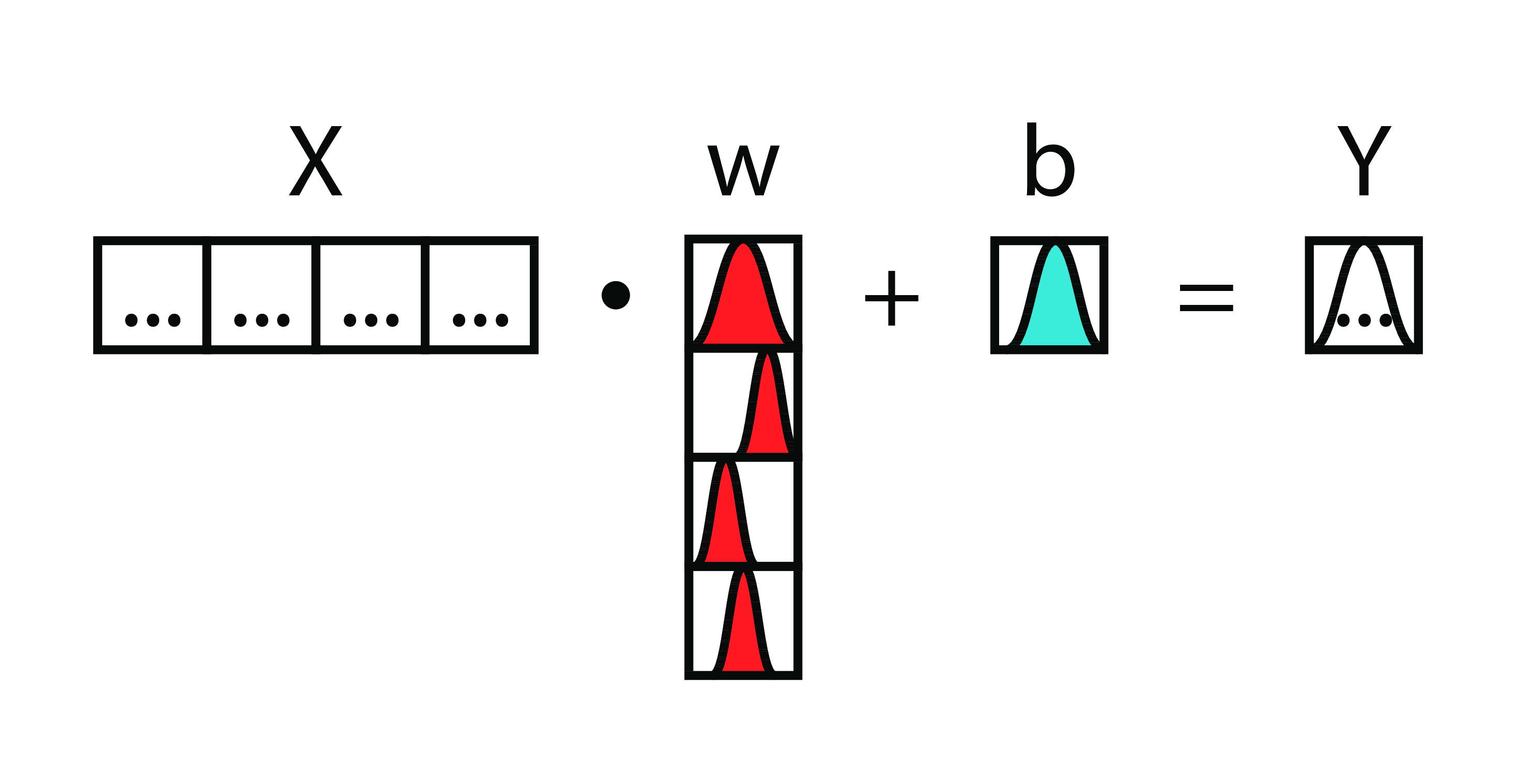
Linear Regression
Function
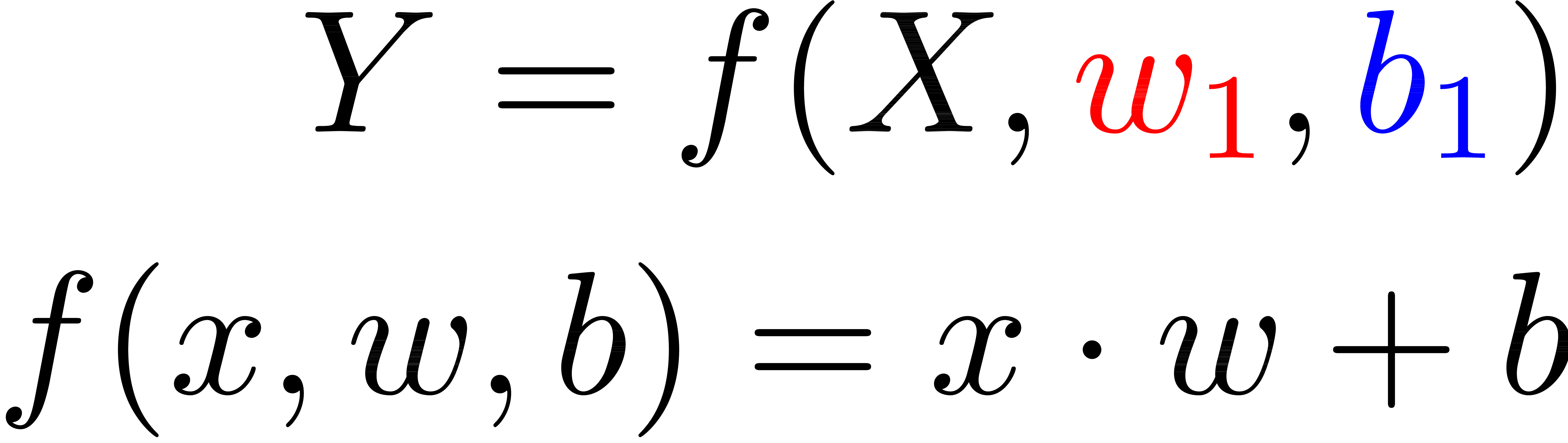
Matrices
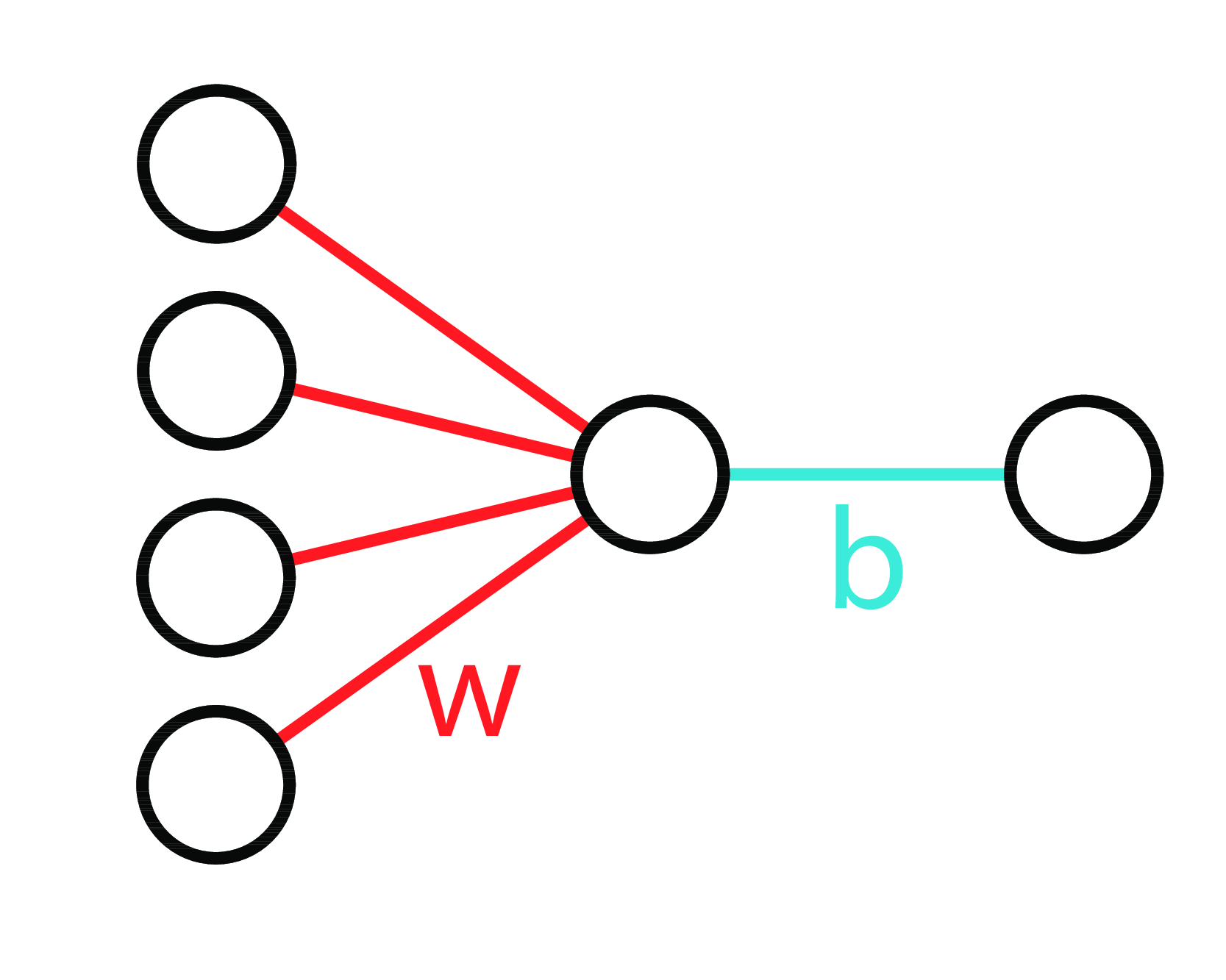
Neural Diagram
LinReg 3 Ways

Logistic Regression
Function
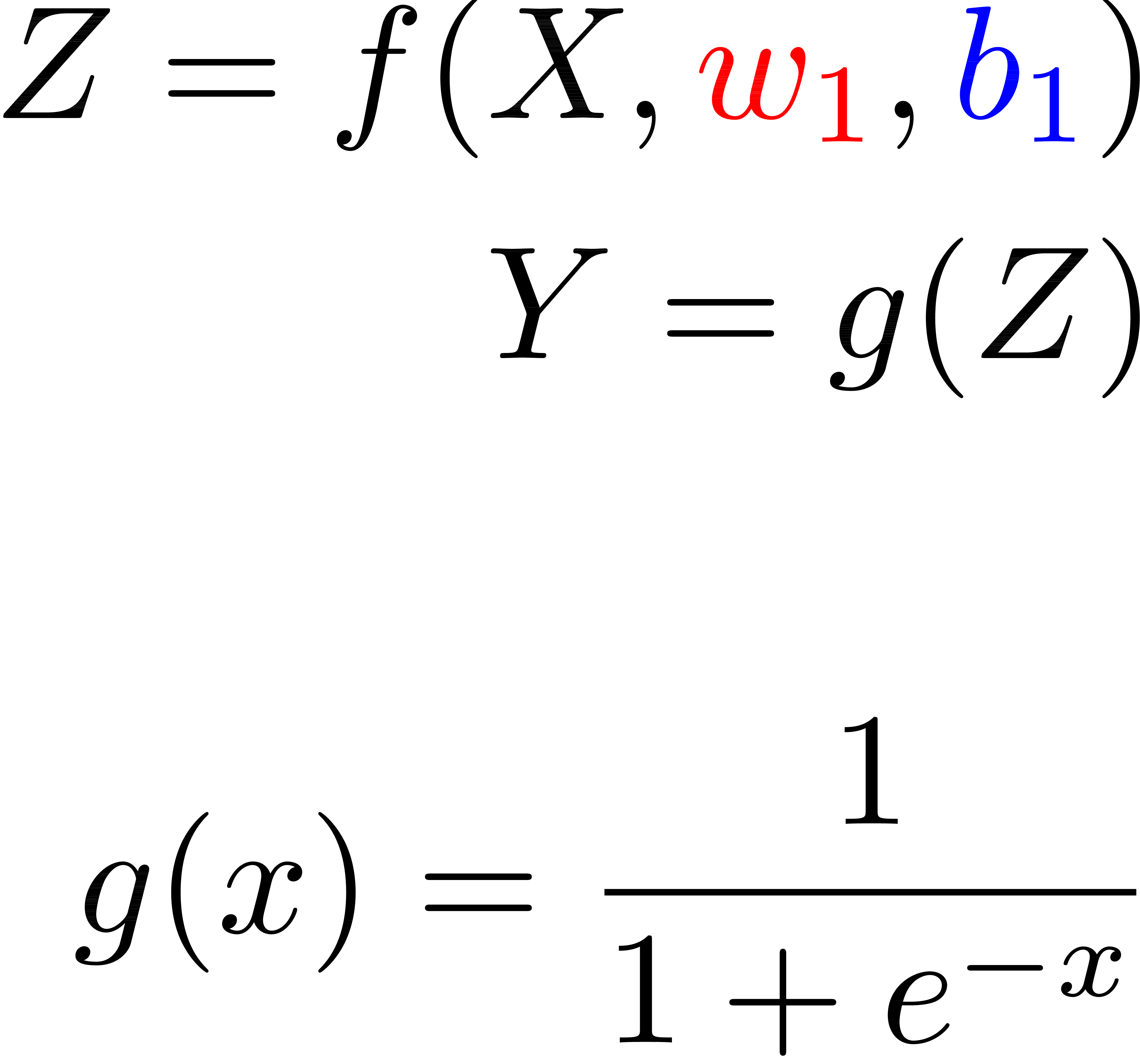
Matrices
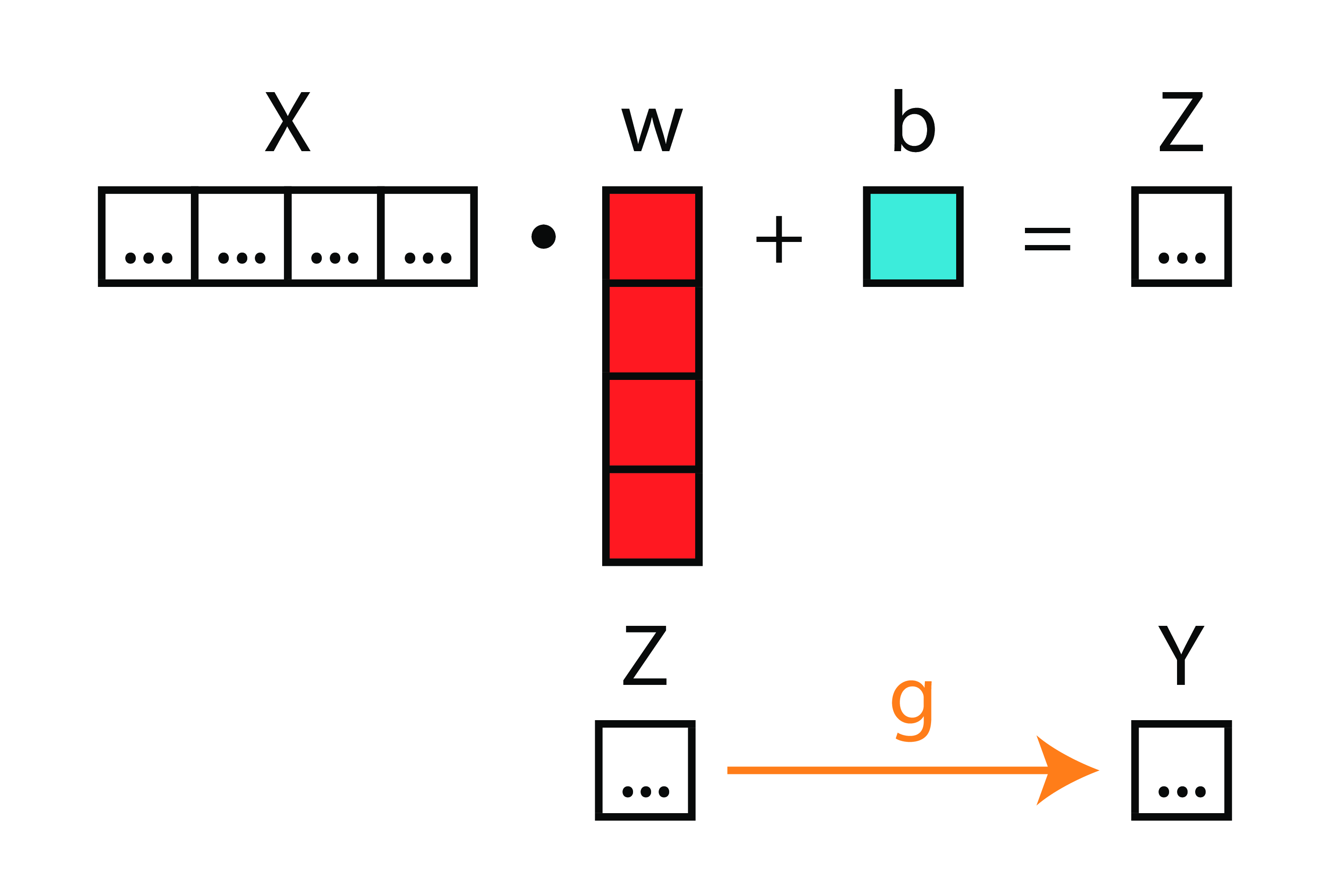
Neural Diagram
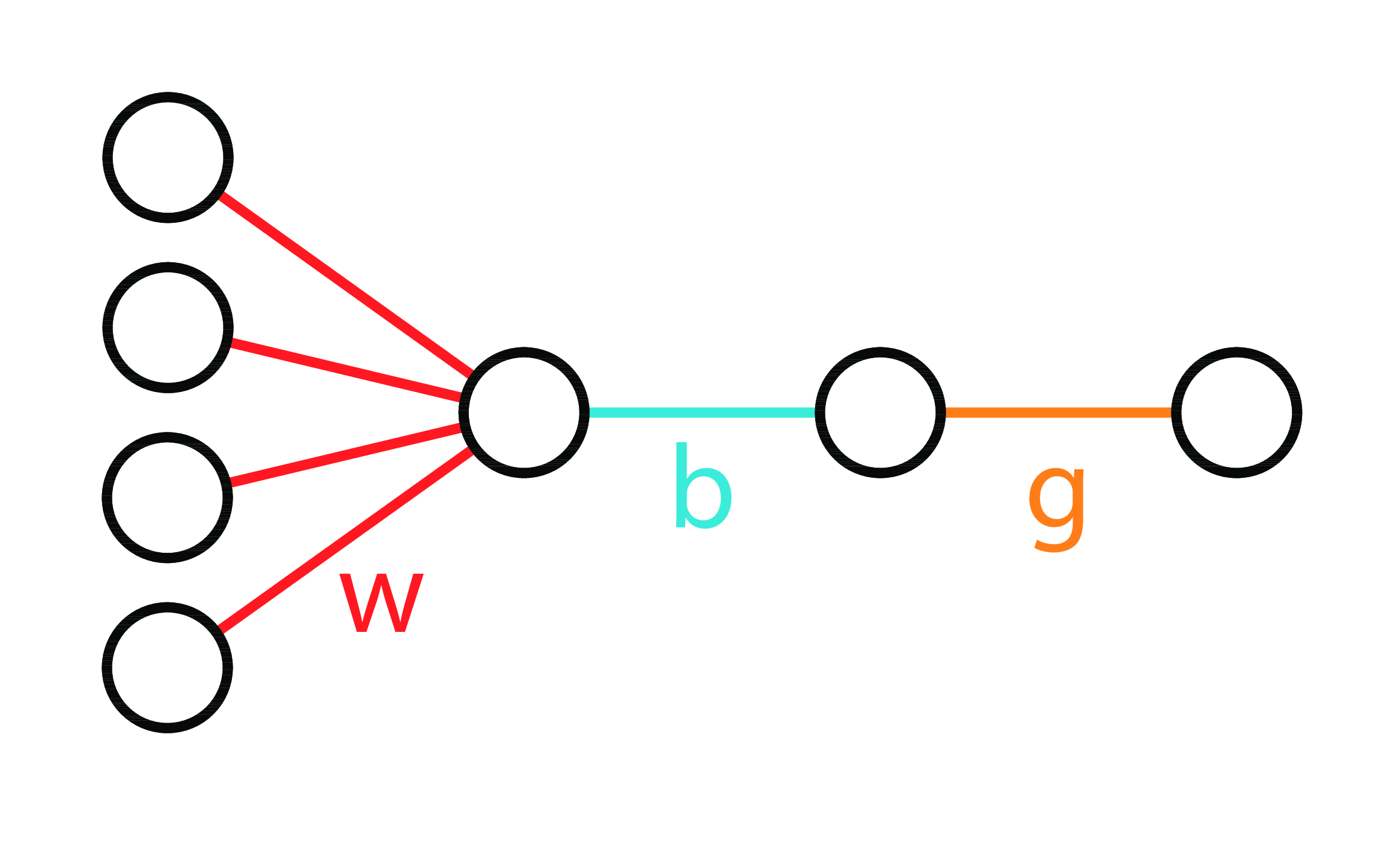
LogReg 3 Ways
Deep Neural Networks
Function
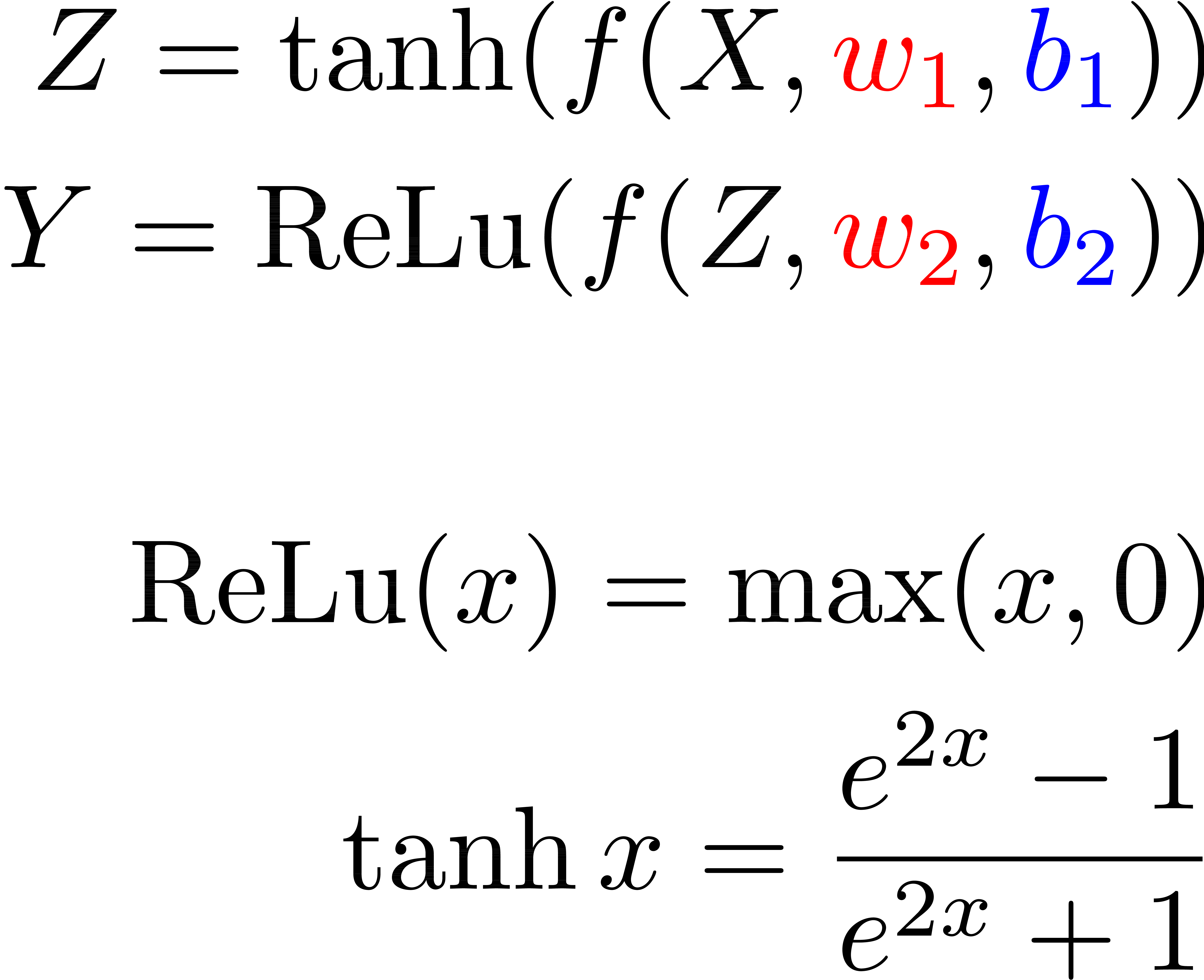
Matrices

Neural Diagram
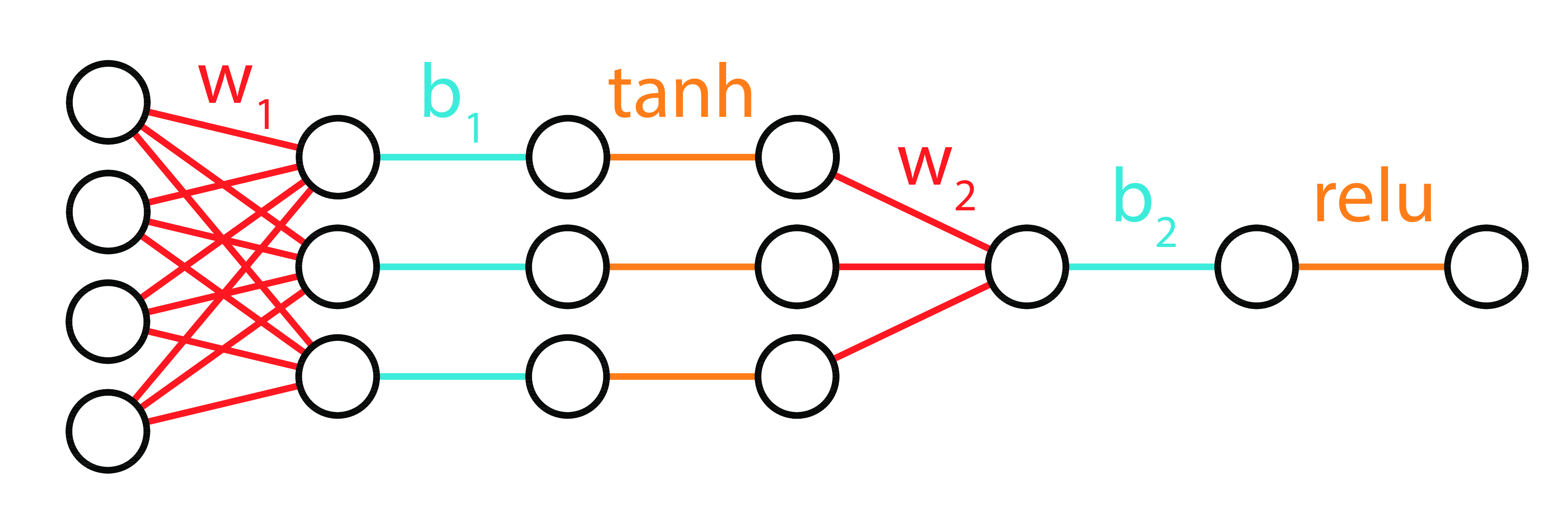
DeepNets 3 Ways
Going Bayesian
Key Idea: Learn probability density over parameter space.
Bayesian Linear Regression
Intuition
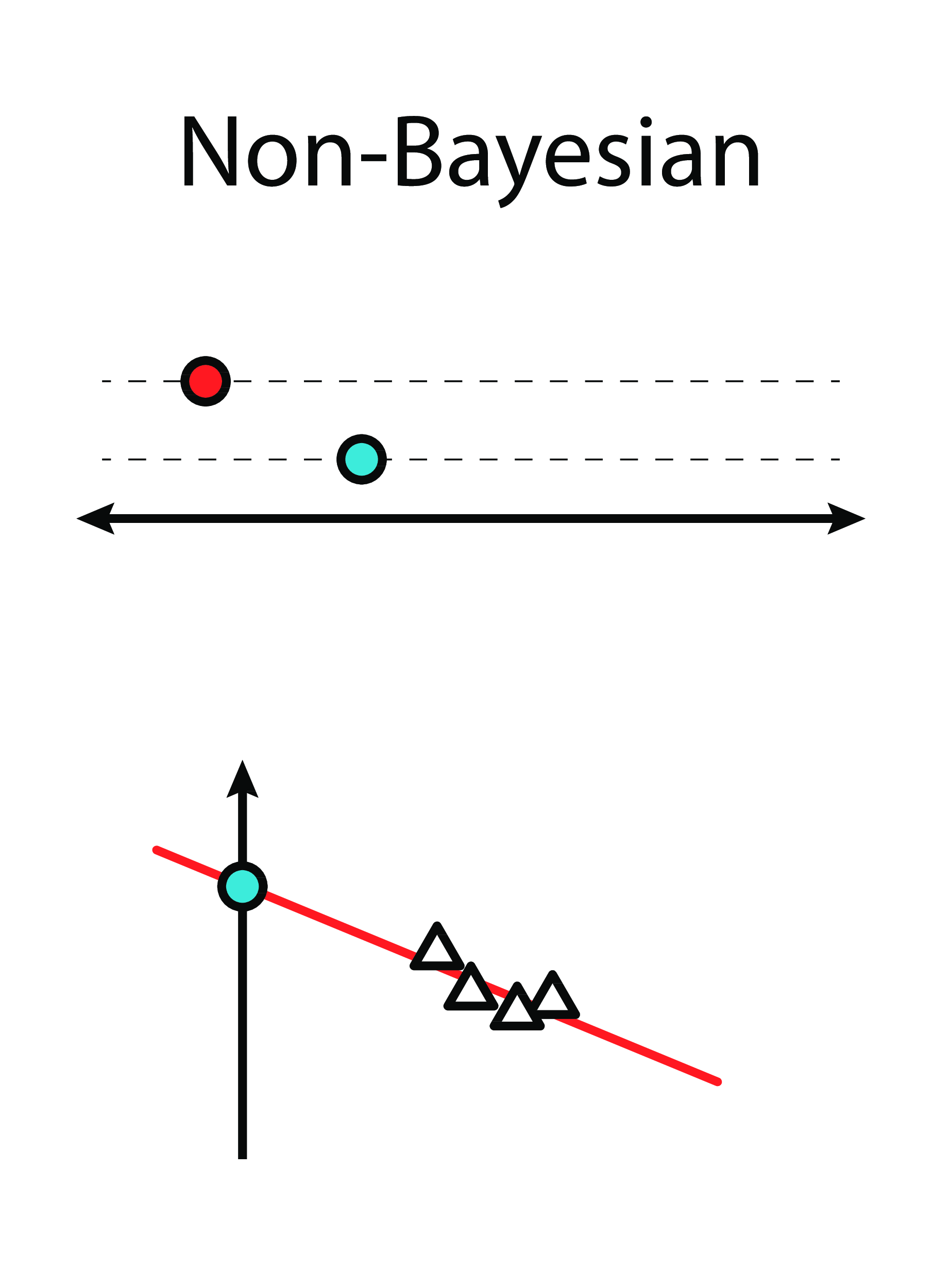 |
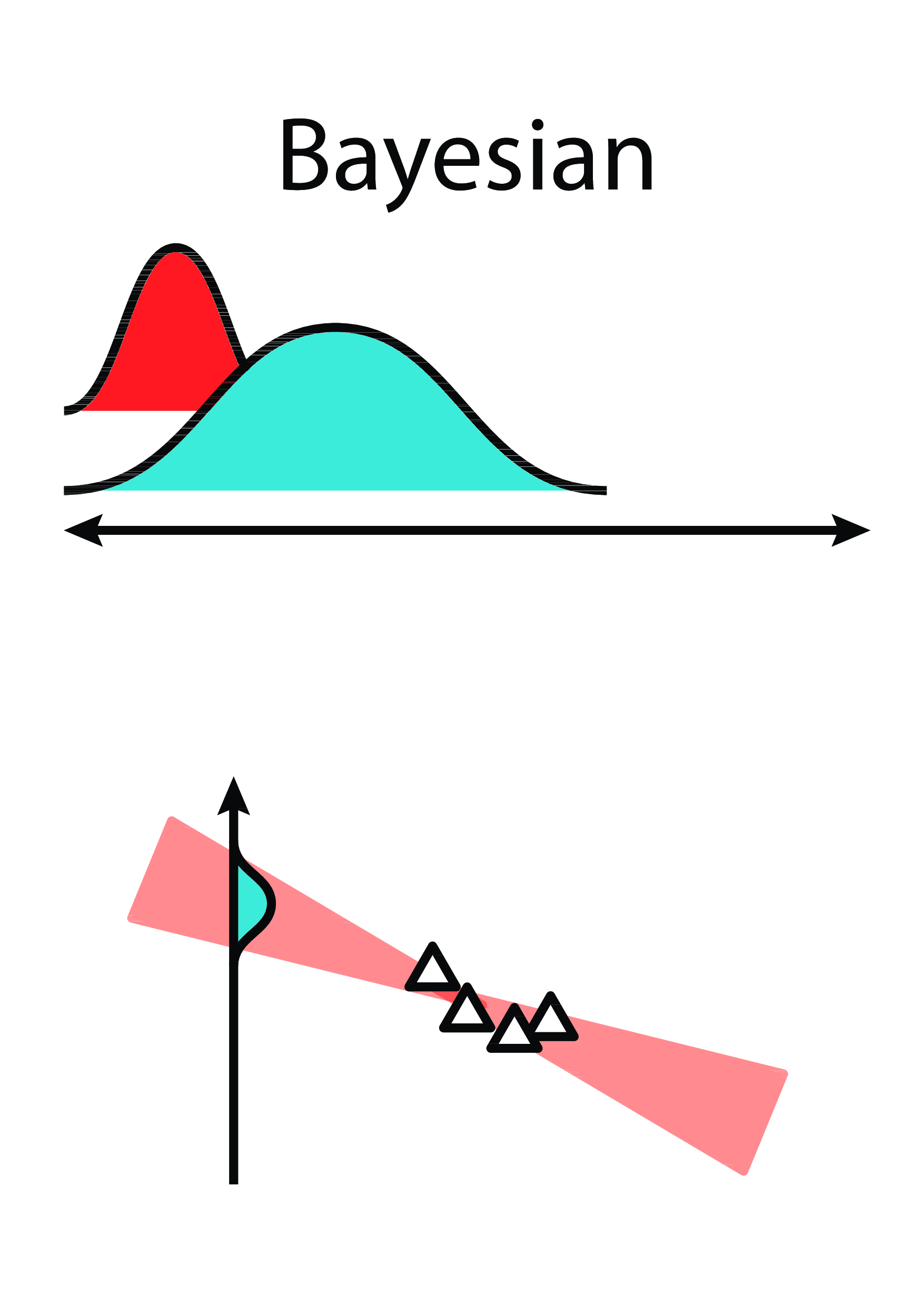 |
From this...

..to this
Bayesian Logistic Regression
From this...
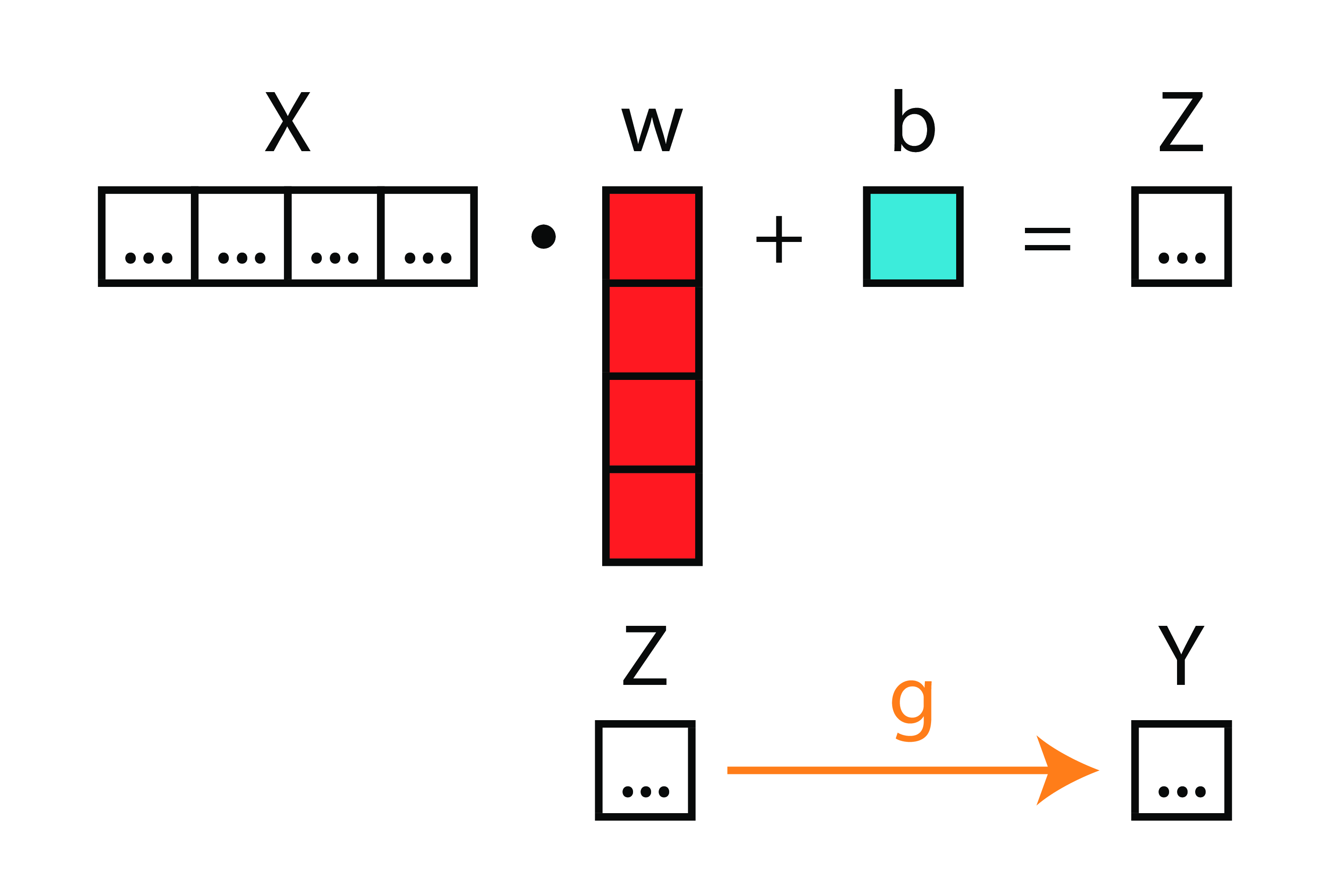
...to this
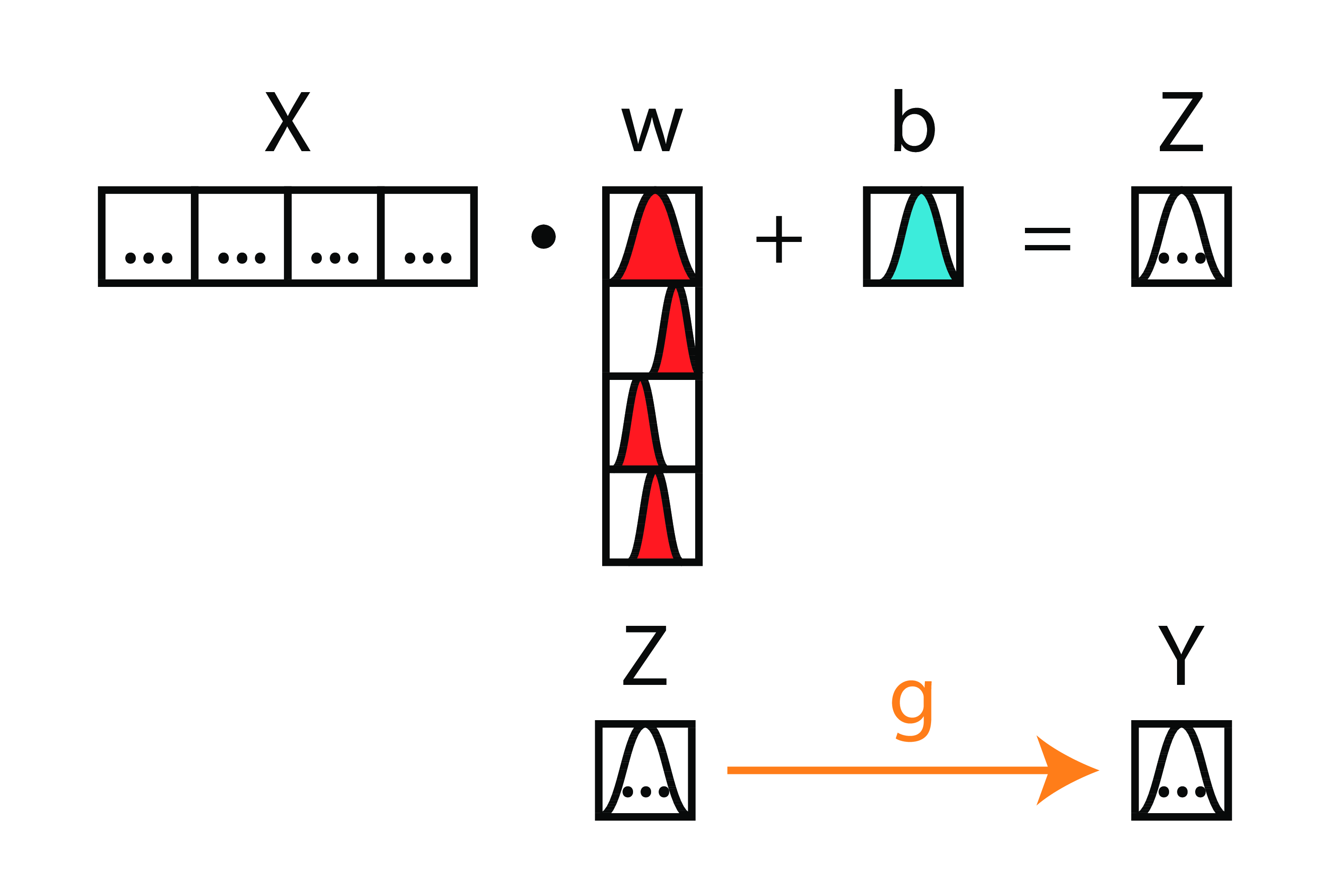
Bayesian Deep Nets
From this...

...to this

Cheat Sheet
Probabilistic Programming in Python. Provides:
- statistical distributions
- sampling algorithms
- syntax
Predict Forest Cover Type
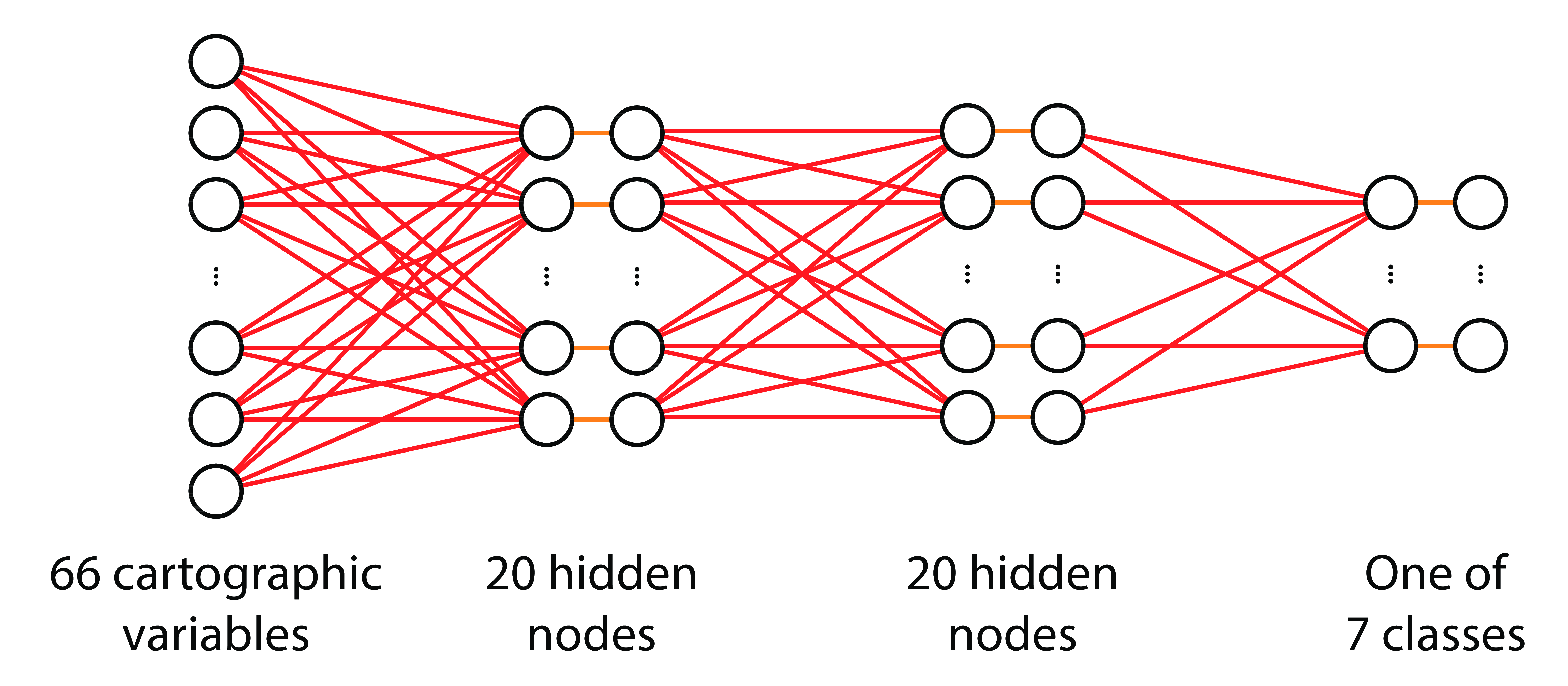
Problem Overview
- UCI ML Repository: Covertype Dataset
- Input: 66 cartographic variables
- Output: one of 7 forest cover types
Network Architecture
import theano.tensor as tt # pymc devs are discussing new backends
import pymc3 as pm
n_hidden = 20
with pm.Model() as nn_model:
# Input -> Layer 1
weights_1 = pm.Normal('w_1', mu=0, sd=1,
shape=(ann_input.shape[1], n_hidden),
testval=init_1)
acts_1 = pm.Deterministic('activations_1',
tt.tanh(tt.dot(ann_input, weights_1)))
# Layer 1 -> Layer 2
weights_2 = pm.Normal('w_2', mu=0, sd=1,
shape=(n_hidden, n_hidden),
testval=init_2)
acts_2 = pm.Deterministic('activations_2',
tt.tanh(tt.dot(acts_1, weights_2)))
# Layer 2 -> Output Layer
weights_out = pm.Normal('w_out', mu=0, sd=1,
shape=(n_hidden, ann_output.shape[1]),
testval=init_out)
acts_out = pm.Deterministic('activations_out',
tt.nnet.softmax(tt.dot(acts_2, weights_out))) # noqa
# Define likelihood
out = pm.Multinomial('likelihood', n=1, p=acts_out,
observed=ann_output)
with nn_model:
s = theano.shared(pm.floatX(1.1))
inference = pm.ADVI(cost_part_grad_scale=s) # approximate inference done using ADVI
approx = pm.fit(100000, method=inference)
trace = approx.sample(5000)
1st Layer Weights

2nd Layer Weights

Output Weights

Class Predictions
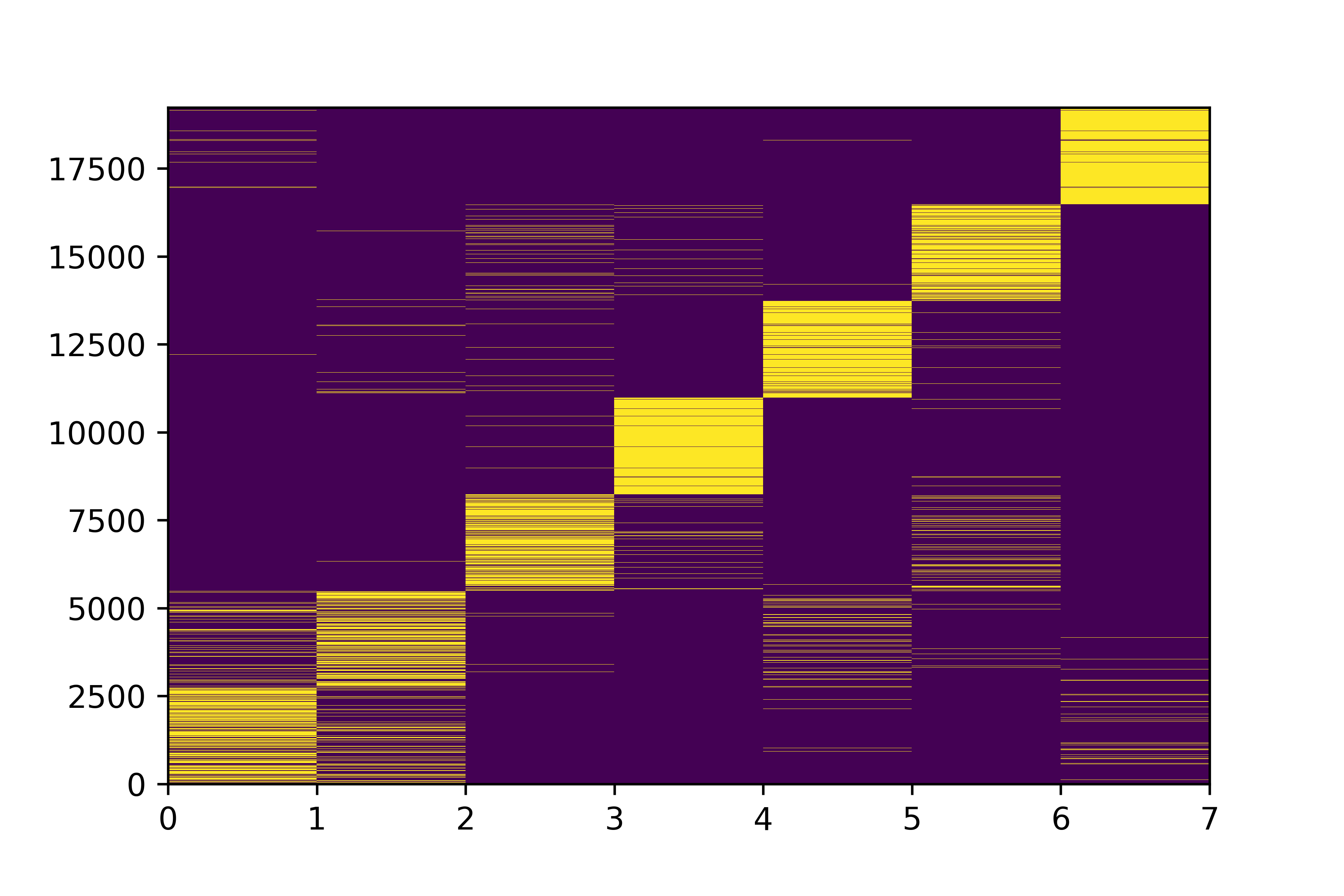
"point estimate"
Class Probabilities
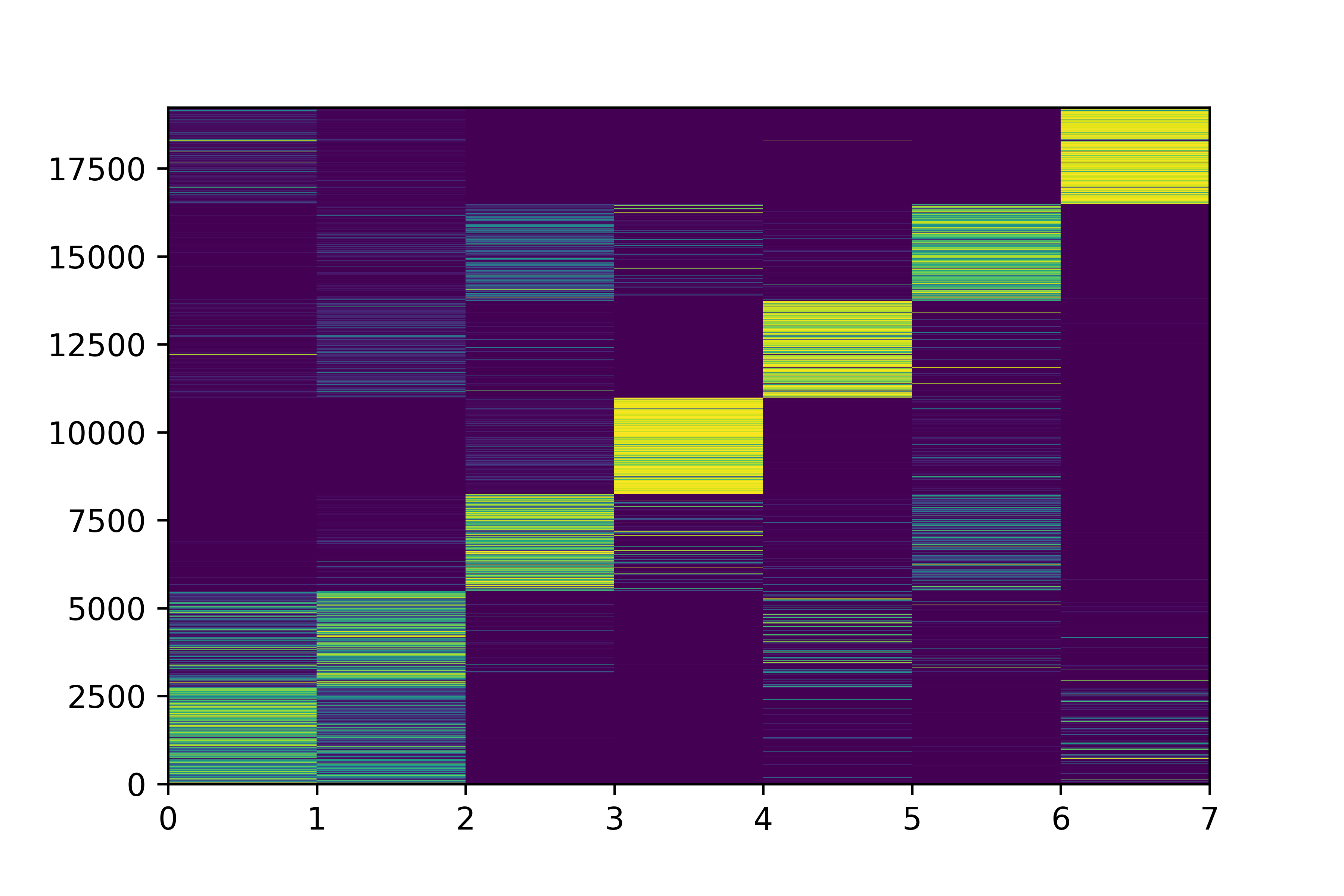
"probabilistic estimate"
Class Uncertainties
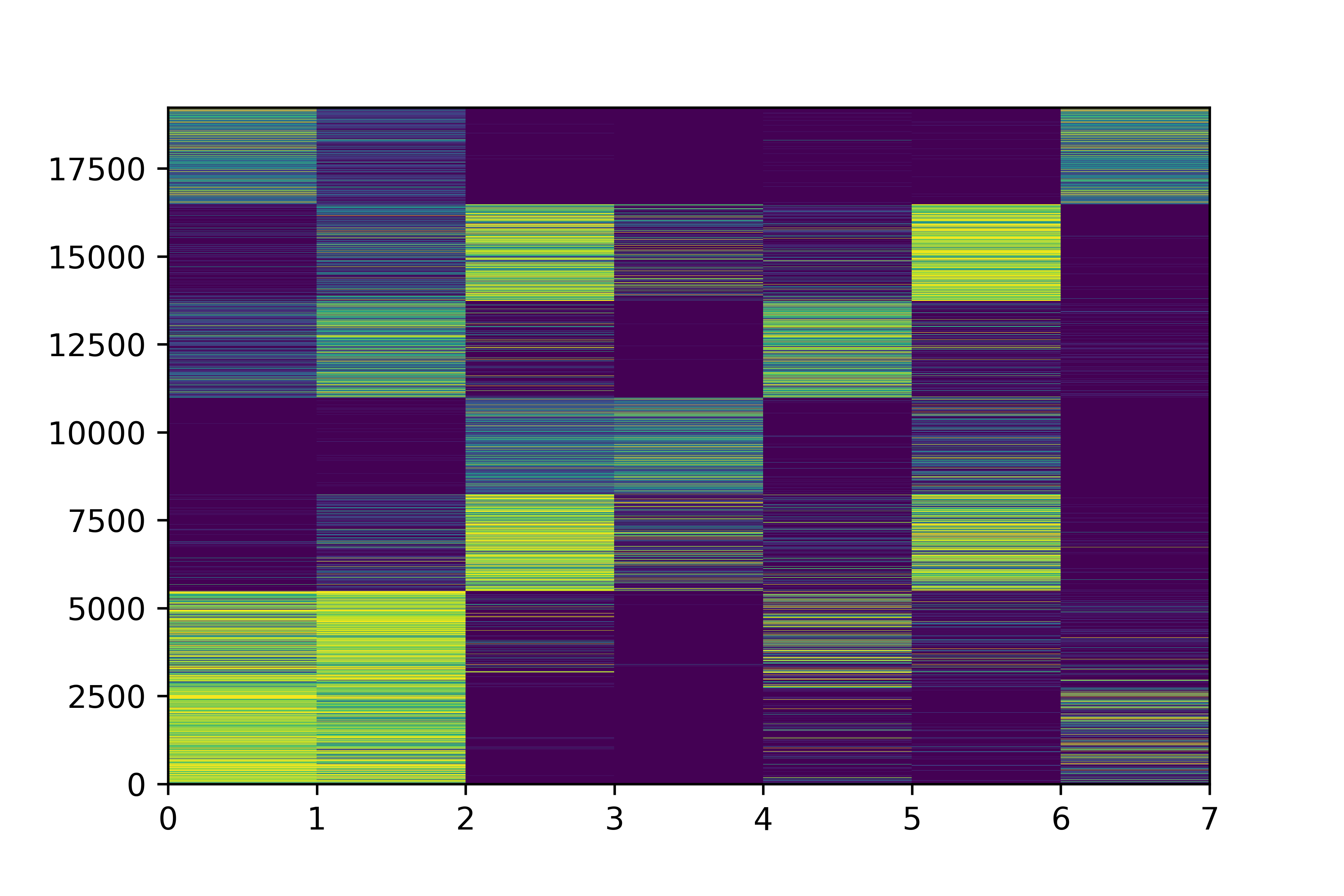
"with uncertainties!"
Take-Home Point 1
Deep Learning is nothing more than compositions of functions on matrices.

Take-Home Point 2
Bayesian deep learning is grounded on learning a probability distribution for each parameter.

Resources
Teachers
- David Duvenaud
- Michelle Fullwood
- Thomas Wiecki
People to Follow
- David MacKay
- Yarin Gal
Thank you!
Source: ericmjl/bayesian-deep-learning-demystified