An Attempt at Demystifying Graph Deep Learning
https://ericmjl.github.io/graph-deep-learning-demystified/
A bit about myself
Professional History
2021-
Principal Data Scientist (Research), Moderna Therapeutics2017-2021
Investigator, Novartis Institutes for BioMedical Research2011-2017
MIT Biological Engineering, Doctor of ScienceI accelerate science to the speed of thought using deep learning, Bayesian statistics, and network science as my main toolkits.
The Hype of Deep Learning:
— Ferenc Huszár (@fhuszar) November 23, 2017
1. Write a post with ML, AI or GAN in the title.
2. post appears at the top of hackernews (despite your best efforts)
3. HN drives tens of thousands of clicks
4. "what's with all the maths? show me pretty pics"
5. <=1% stay for longer than a minute
I'm out to solve Point #4.
Let's talk about graphs
When you think of graphs, think networks❗️
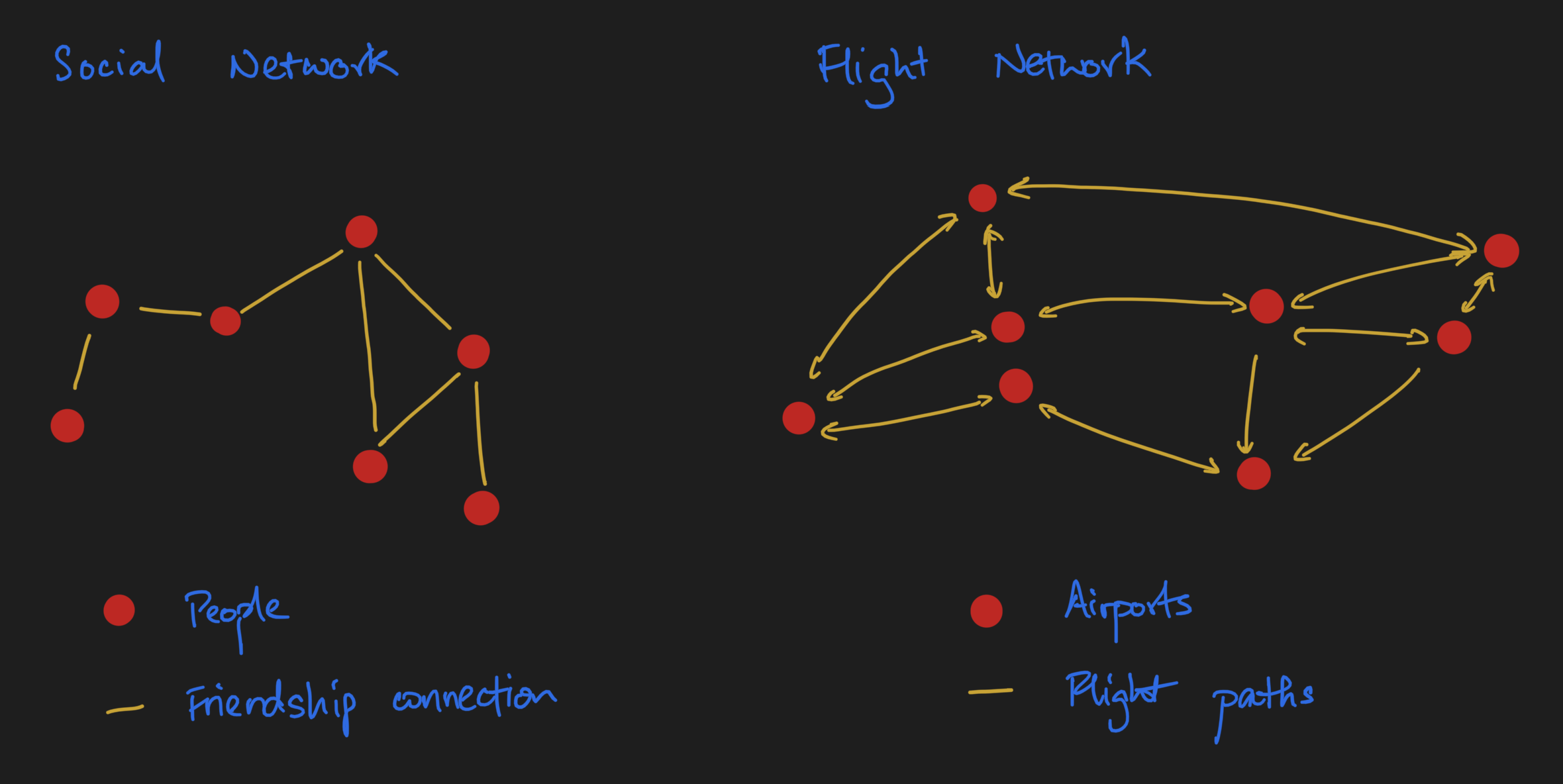
All of deep learning operates on arrays.

How do we represent graphs as arrays?
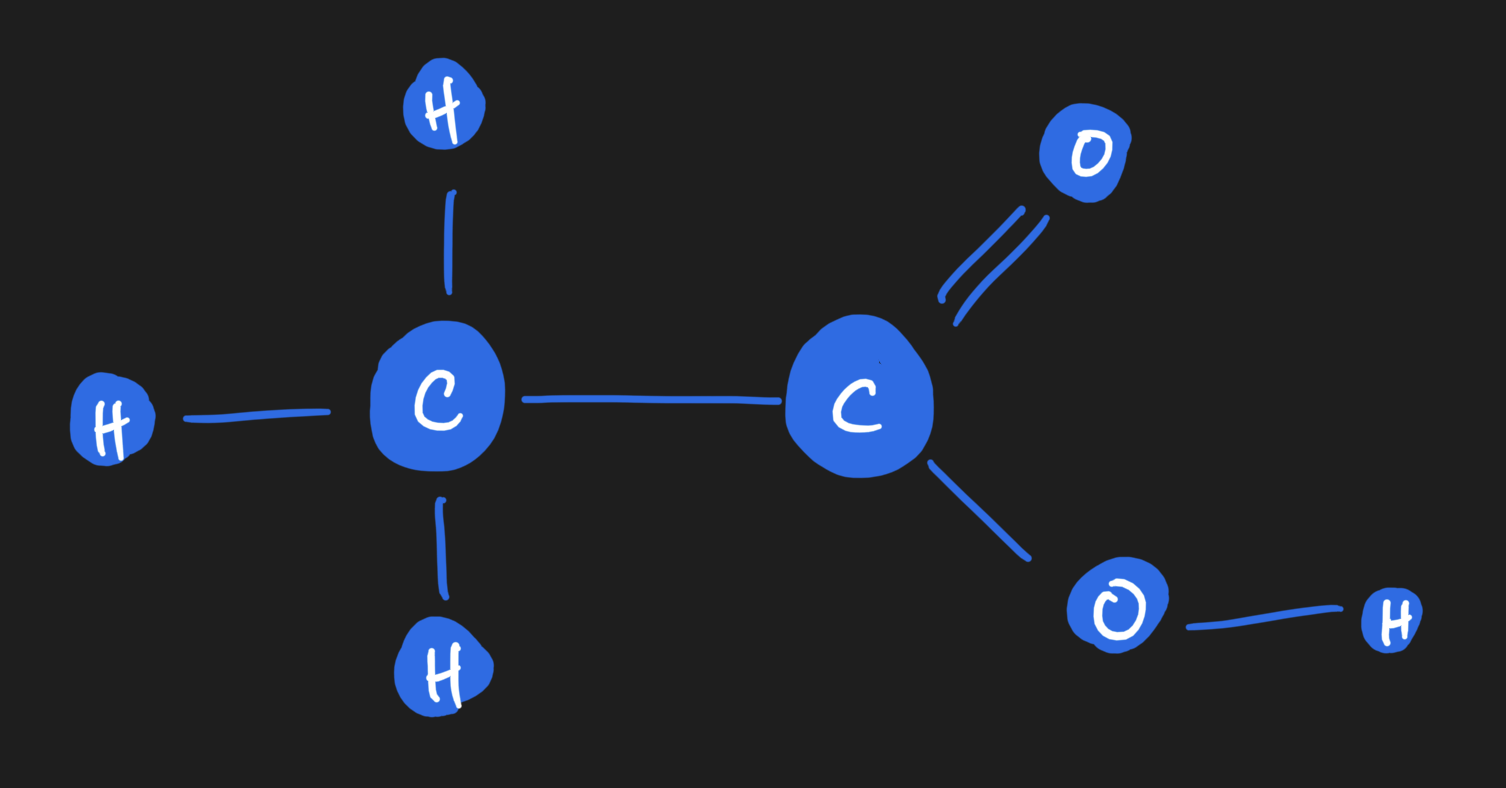
Let's look at an minimally complex anchoring example.
Here is a molecule, represented as a graph.
Here is the same molecule, with numerical properties.
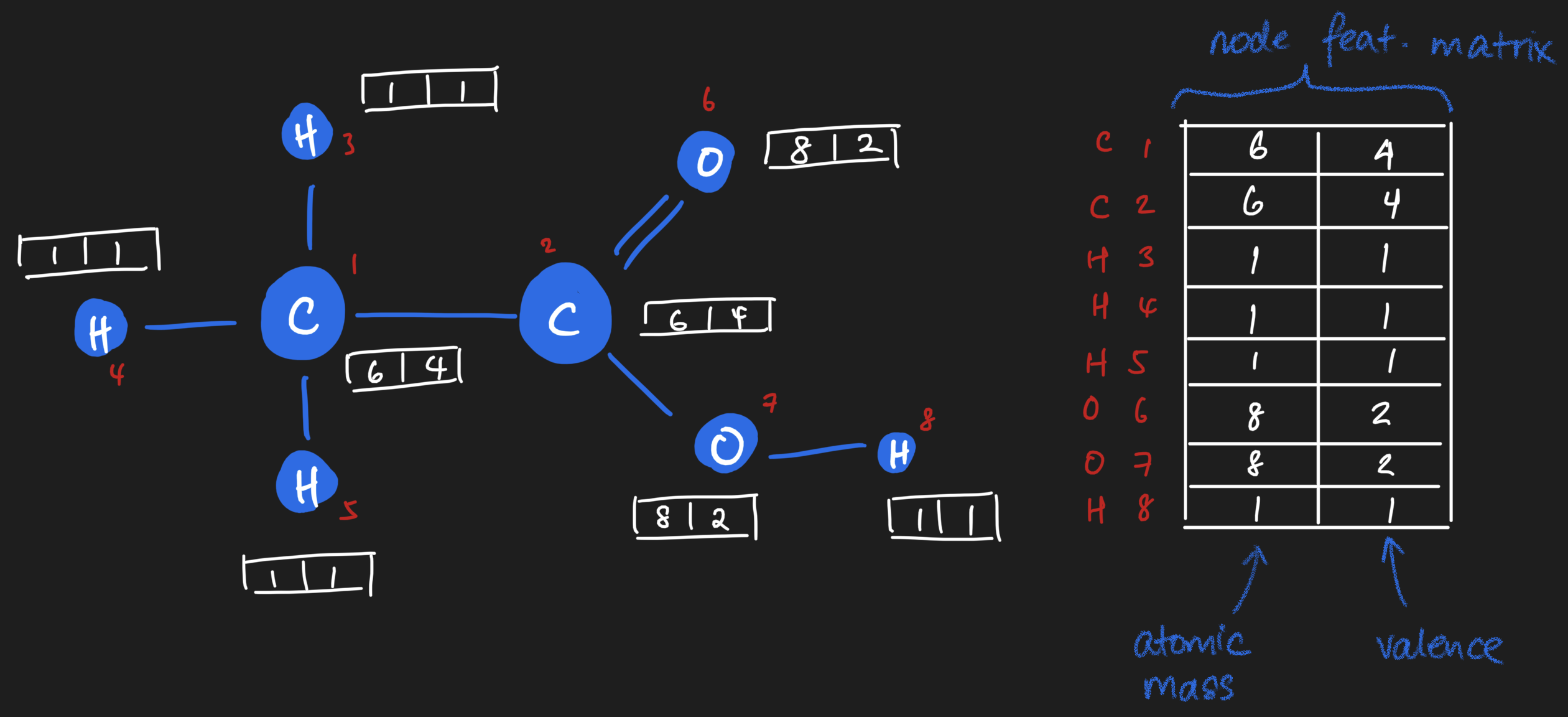
The table on the right is the node feature matrix.

We know how to represent nodes as arrays.
What about edges?
The adjacency matrix lets us represent edges.
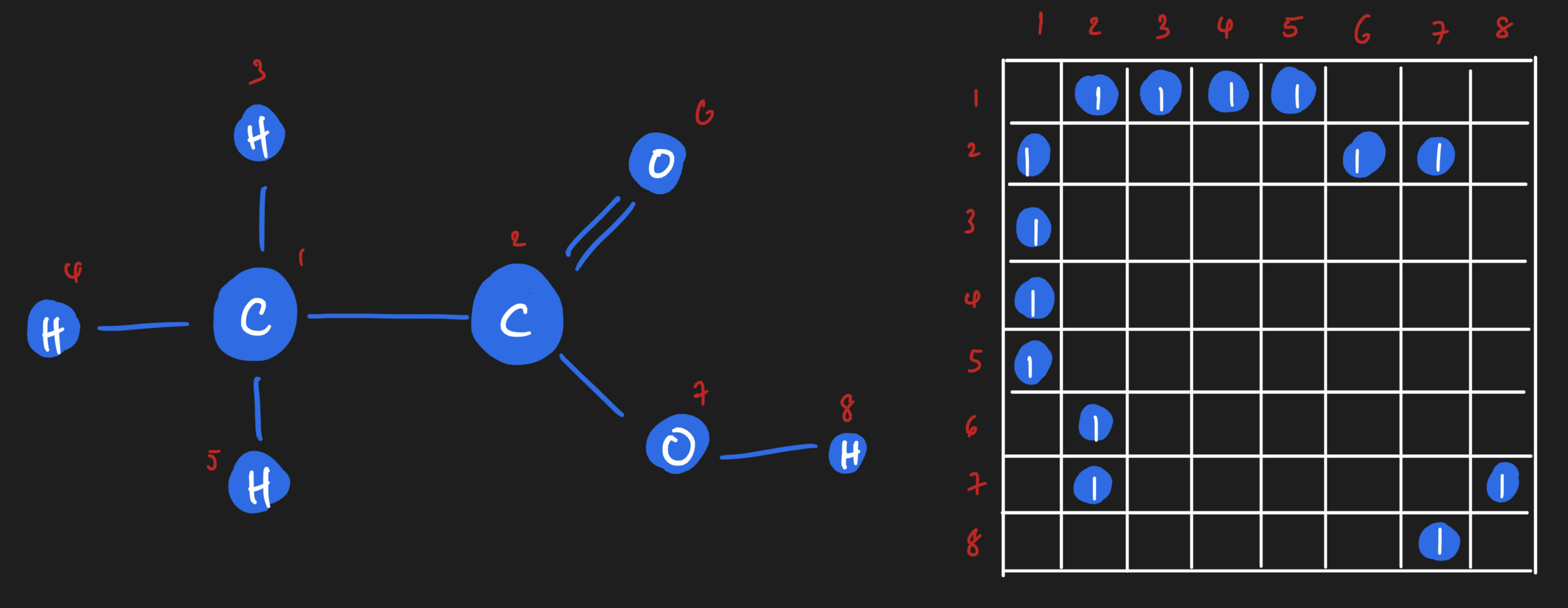
This adjacency matrix shows 1️⃣s anywhere an edge exists.

Matrix is symmetric b/c graph is undirected!
This adjacency matrix shows the number of bonds between atoms.
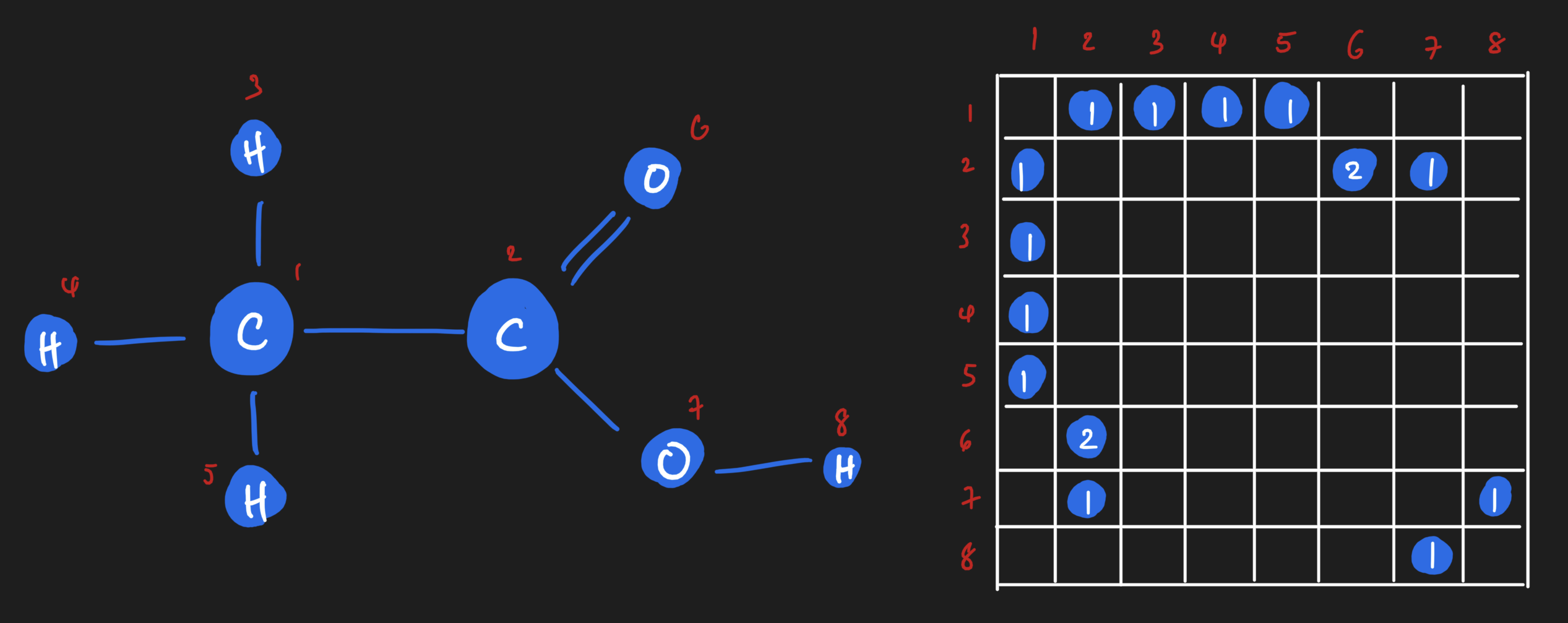
Summary
- Nodes can be represented in a node feature matrix.
- Edges can be represented in an adjacency matrix.
Those two matrices, together, give a numerical representation of the graph.
Let's talk about message passing
Message passing on graphs is nothing more than dot products of matrices.
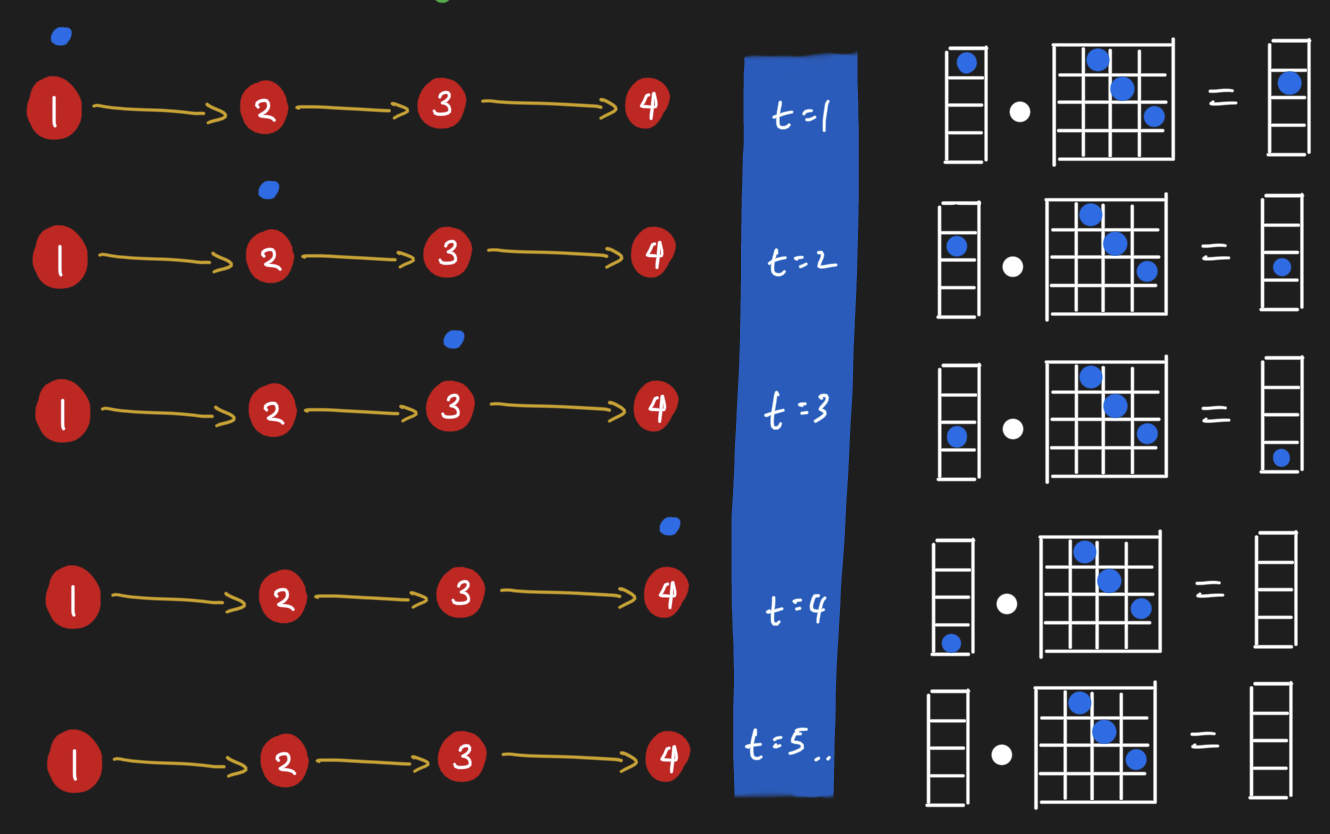 Please ignore the fact that a transpose is necessary to make this work.
Please ignore the fact that a transpose is necessary to make this work.
Message passing on graphs is nothing more than dot products of matrices.
import jax.numpy as np
def message_passing(A, F):
return np.dot(A, F)
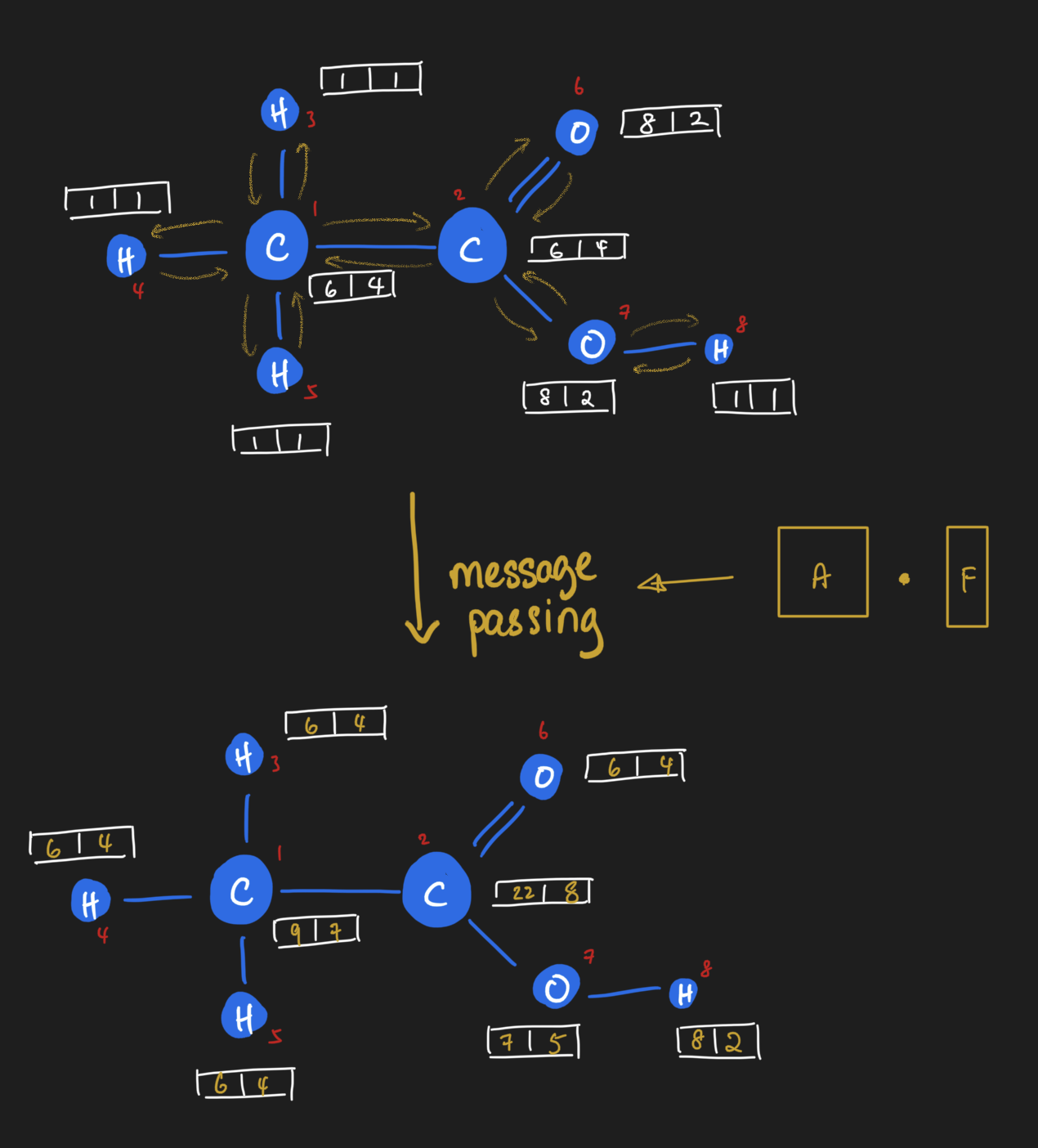
So how do we connect message passing to neural networks?
We can take the result of message passing and feed them through neural network operations.
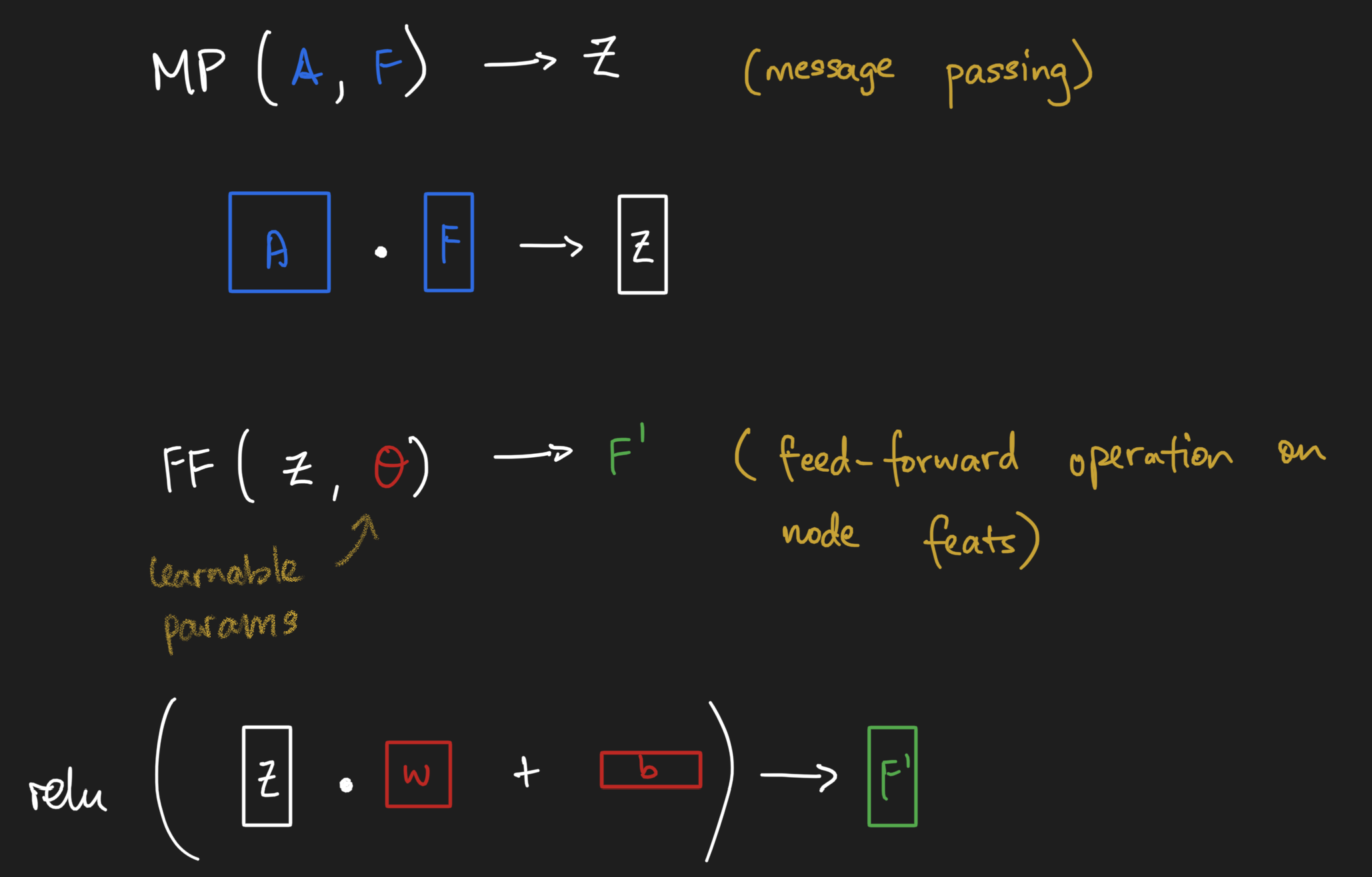
Sometimes, we need an operation to summarize nodes.

Putting everything together...
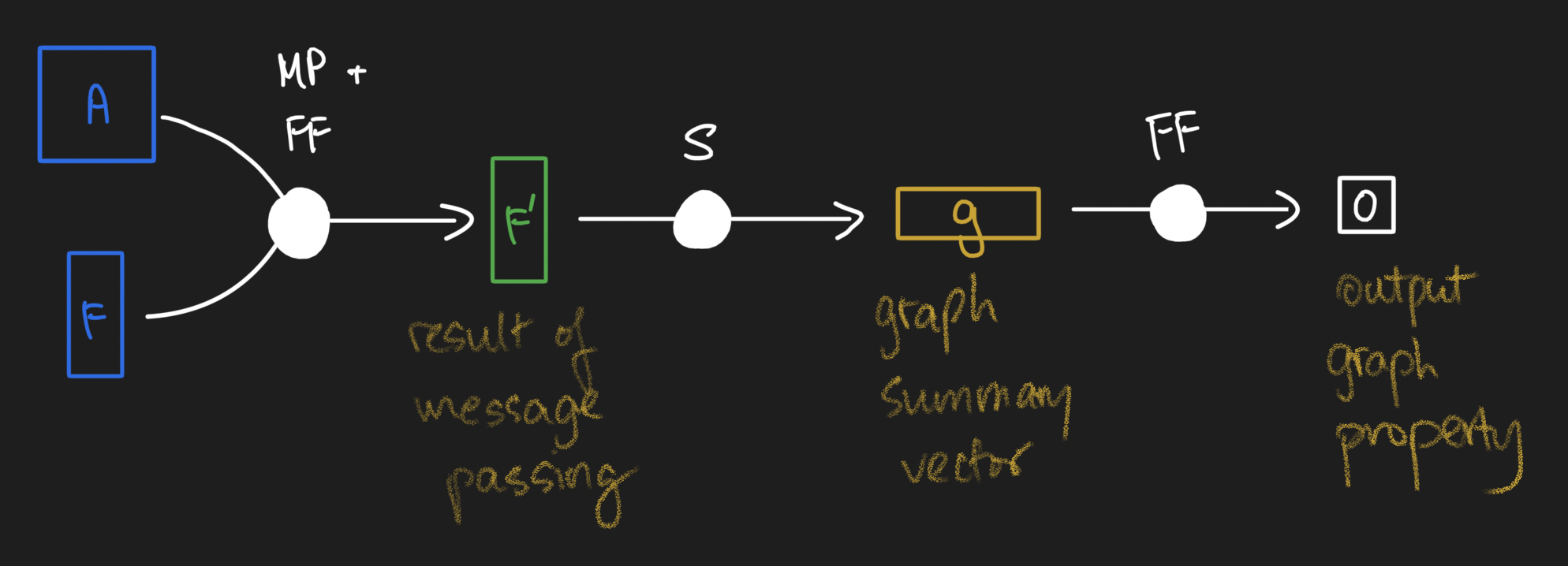
And that, my friends, is graph deep learning demystified!
A = np.array(...) # some NumPy array
F = np.array(...) # some NumPy array
G = (A, F)
def mp(G):
A, F = G
Z = np.dot(A, F)
return (A, Z)
def graph_summary(G):
_, F = G
return np.sum(F, axis=0)
def gnn_feedforward(params, G):
_, F = G
w, b = params
return relu(np.dot(F, w) + b)
def feedforward(params, x):
w, b = params
return relu(np.dot(x, w) + b)
def model(params, G):
G = mp(G)
G = gnn_feedforward(G, params["gnn"])
g = graph_summary(G)
return feedforward(params["ff"], g)
Bonus fact!
Regular convlution operations look a ton like message passing!
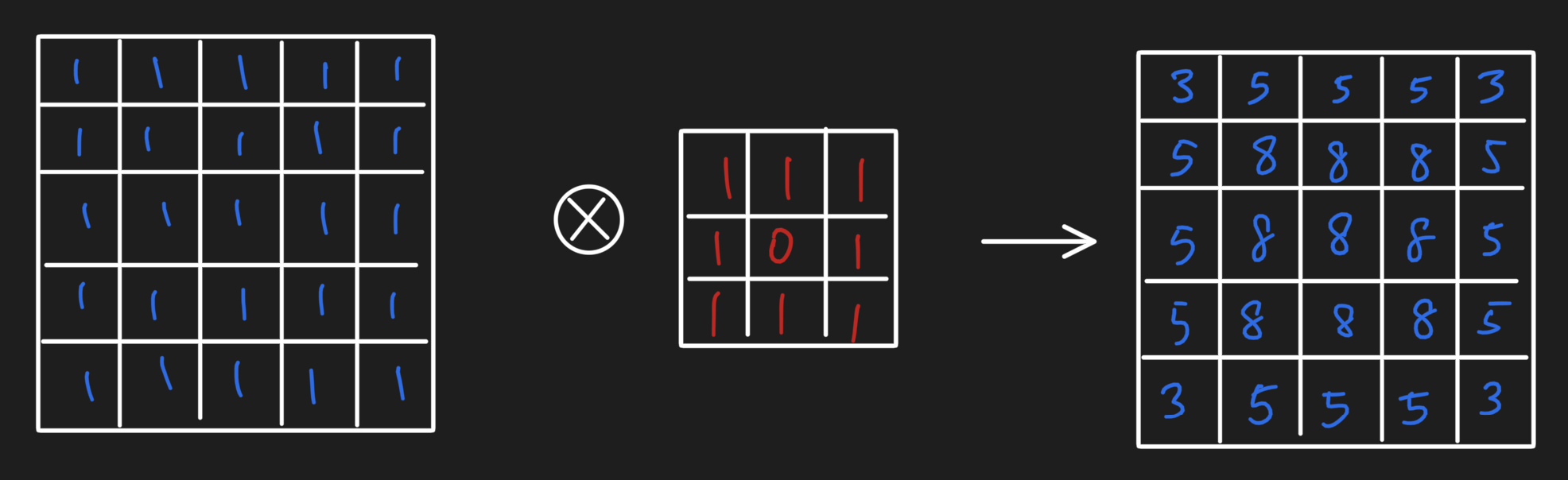
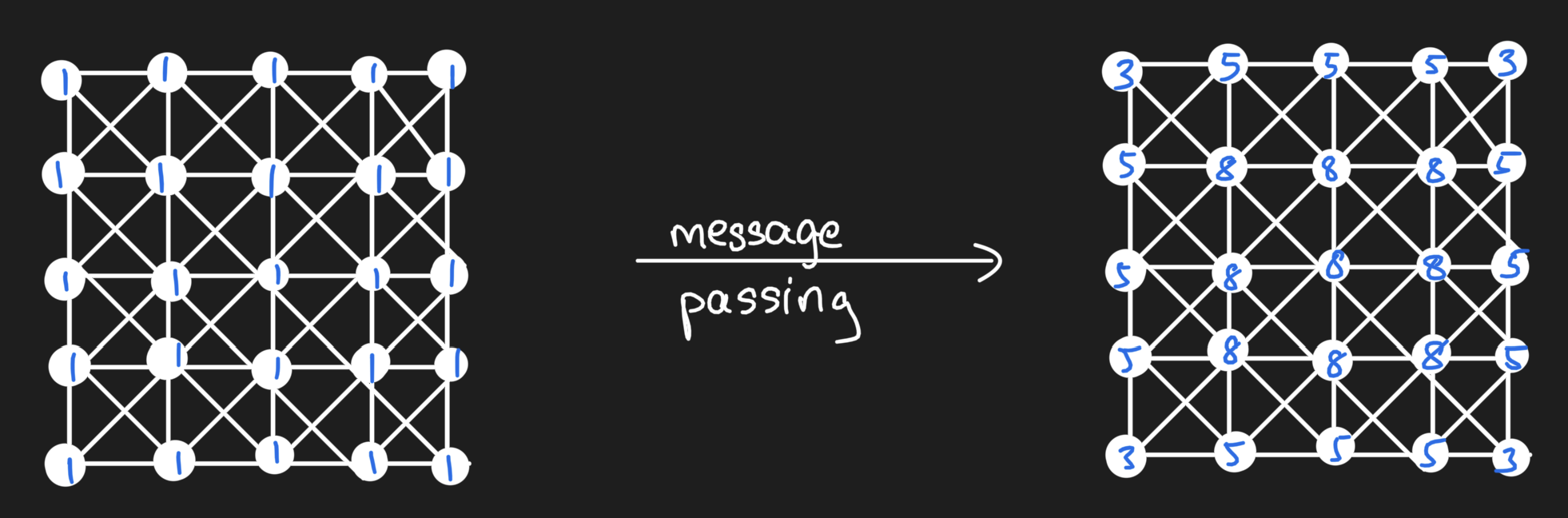
When do we use what types of neural networks?
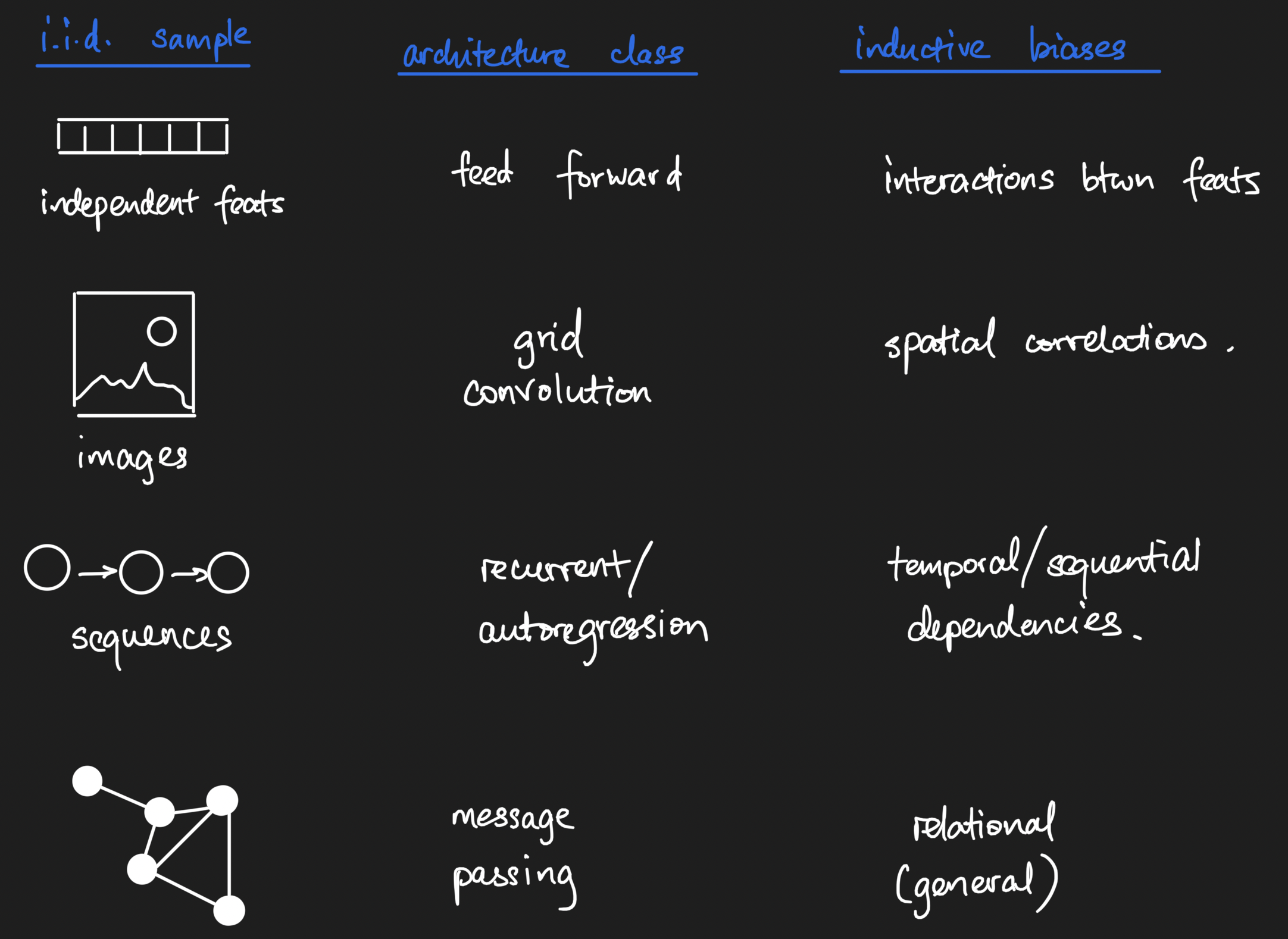 Your inductive biases should be encoded in the model.
Your inductive biases should be encoded in the model.
Summary
Graphs can be represented as matrices.
Node Feature Matrix

Adjacency Matrix

Graph deep learning is anchored on message passing.
