Eric J Ma's Website
written by Eric J. Ma on 2019-07-23 | tags: data science statistics distributions
It’s mainly because they are the generalization of two distributions, the Cauchy and Gaussian. Come learn more!
The Student’s T distribution is the generalization of the Gaussian and Cauchy distributions. How so? Basically by use of its "degrees of freedom" ($df$) parameter.
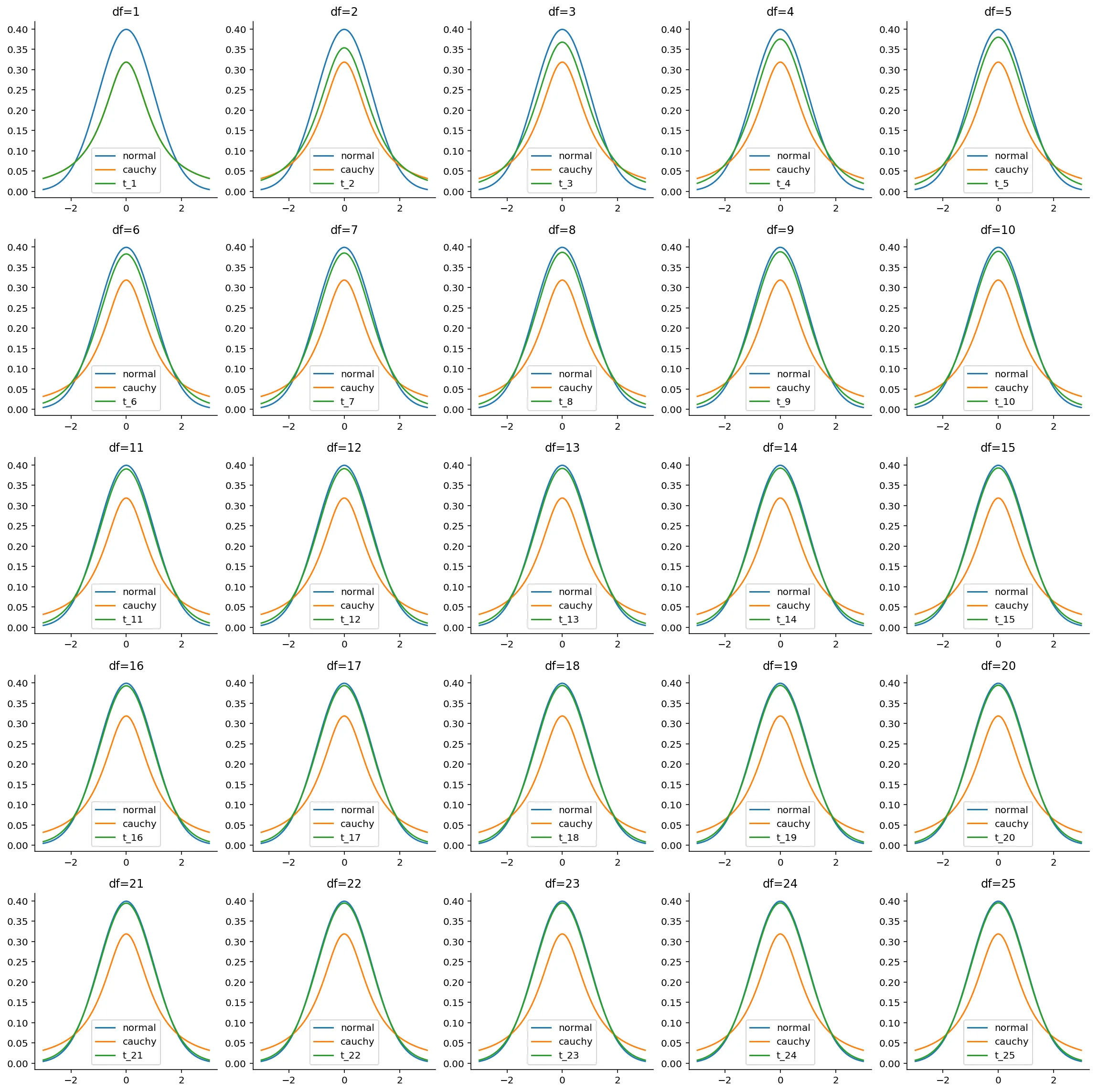
If we plot the probability density functions of the T distribution with varying degrees of freedom, and compare them to the Cauchy and Gaussian distributions, we get the following:
Notice that when $df=1$, the T distribution is identical to the Cauchy distribution, and that as $df$ increases, it gradually becomes more and more like the Normal distribution. At $df=30$, we can consider it to be approximately enough Gaussian.
On its own, this is already quite useful; when placed in the context of a hierarchical Bayesian model, that’s when it gets even more interesting! In a hierarchical Bayesian model, we are using samples to estimate group-level parameters, but constraining group parameters to vary mostly like each other, unless evidence in the data suggests otherwise. If we allow the $df$ parameter to vary, then if some groups look more Cauchy while other groups look more Gaussian, this can be flexibly captured in the model.
Cite this blog post:
@article{
ericmjl-2019-t-distributed-likelihoods-are-kind-of-neat,
author = {Eric J. Ma},
title = {T-distributed likelihoods are kind of neat},
year = {2019},
month = {07},
day = {23},
howpublished = {\url{https://ericmjl.github.io}},
journal = {Eric J. Ma's Blog},
url = {https://ericmjl.github.io/blog/2019/7/23/t-distributed-likelihoods-are-kind-of-neat},
}
I send out a newsletter with tips and tools for data scientists. Come check it out at Substack.
# TODO(eric): learn how to learn anything. feb 2027.
If you would like to sponsor the coffee that goes into making my posts, please consider GitHub Sponsors!